题目内容
已知tanα=-
,α∈(
,π),则cosα= .
| 3 |
| π |
| 2 |
考点:三角函数的化简求值,同角三角函数间的基本关系
专题:三角函数的求值
分析:直接利用三角函数值求出角的大小,然后求解即可.
解答:
解:tanα=-
,α∈(
,π),
∴α=
,
则cosα=cos
=-
.
故答案为:-
.
| 3 |
| π |
| 2 |
∴α=
| 2π |
| 3 |
则cosα=cos
| 2π |
| 3 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查三角函数的化简求值,也可以通过同角三角函数的基本关系式求解,考查计算能力.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
若直线AB的斜率是
,将直线AB绕A点按逆时针方向旋转45°后,所得直线的倾斜角是( )
| 3 |
| A、105° | B、15° |
| C、75° | D、120° |
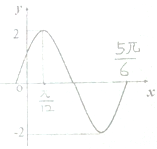 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<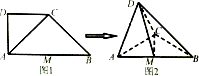 如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.
如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.