题目内容
17.对于无穷数列{an},记T={x|x=aj-ai,i<j},若数列{an}满足:“存在t∈T,使得只要am-ak=t(m,k∈N*且m>k),必有am+1-ak+1=t”,则称数列{an}具有性质P(t).(Ⅰ)若数列{an}满足${a_n}=\left\{{\begin{array}{l}{2n,n≤2}\\{2n-5,n≥3}\end{array}}\right.$判断数列{an}是否具有性质P(2)?是否具有性质P(4)?
(Ⅱ)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(Ⅲ)已知{an}是各项为正整数的数列,且{an}既具有性质P(2),又具有性质P(5),求证:存在整数N,使得aN,aN+1,aN+2,…,aN+k,…是等差数列.
分析 (Ⅰ)由${a_n}=\left\{{\begin{array}{l}{2n,n≤2}\\{2n-5,n≥3}\end{array}}\right.$可得a2-a1=2,但a3-a2=-1≠2,数列{an}不具有性质P(2);同理可判断数列{an}具有性质P(4).
(Ⅱ)举例“周期数列1,1,2,2,1,1,2,2,…,T={-1,0,1}是有限集,利用新定义可证数列{an}不具有性质P(0),即不充分性成立;再证明其必要性即可.
(Ⅲ)依题意,数列{an}是各项为正整数的数列,且{an}既具有性质P(2),又具有性质P(5),可证得存在整数N,使得aN,aN+1,aN+2,…,aN+k,…是等差数列.
解答 (本小题满分13分)
解:(Ⅰ)∵${a_n}=\left\{{\begin{array}{l}{2n,n≤2}\\{2n-5,n≥3}\end{array}}\right.$,a2-a1=2,但a3-a2=-1≠2,数列{an}不具有性质P(2);
同理可得,数列{an}具有性质P(4).
(Ⅱ)(不充分性)对于周期数列1,1,2,2,1,1,2,2,…,T={-1,0,1}是有限集,但是由于a2-a1=0,a3-a2=1,
所以不具有性质P(0);
(必要性)因为数列{an}具有性质P(0),
所以一定存在一组最小的且m>k,满足am-ak=0,即am=ak
由性质P(0)的含义可得am+1=ak+1,am+2=ak+2,…,a2m-k-1=am-1,a2m-k=am,…
所以数列{an}中,从第k项开始的各项呈现周期性规律:ak,ak+1,…,am-1为一个周期中的各项,
所以数列{an}中最多有m-1个不同的项,
所以T最多有$C_{m-1}^2$个元素,即T是有限集.
(Ⅲ)因为数列{an}具有性质P(2),数列{an}具有性质P(5),
所以存在M′、N′,使得aM'+p-aM'=2,aN'+q-aN'=5,其中p,q分别是满足上述关系式的最小的正整数,
由性质P(2),P(5)的含义可得,aM'+p+k-aM'+k=2,aN'+q+k-aN'+k=5,
若M'<N',则取k=N'-M',可得aN'+p-aN'=2;
若M'>N',则取k=M'-N',可得aM'+q-aM'=5.
记M=max{M',N'},则对于aM,有aM+p-aM=2,aM+q-aM=5,显然p≠q,
由性质P(2),P(5)的含义可得,aM+p+k-aM+k=2,aN+q+k-aN+k=5,
所以aM+qp-aM=(aM+qp-aM+(q-1)p)+(aM+(q-1)p-aM+(q-2)p)+…+(aM+p-aM)=2qaM+qp-aM=(aM+pq-aM+(p-1)q)+(aM+(p-1)q-aM+(p-2)q)+…+(aM+q-aM)=5p
所以aM+qp=aM+2q=aM+5p.
所以2q=5p,
又p,q是满足aM+p-aM=2,aM+q-aM=5的最小的正整数,
所以q=5,p=2,aM+2-aM=2,aM+5-aM=5,
所以,aM+2+k-aM+k=2,aM+5+k-aM+k=5,
所以,aM+2k=aM+2(k-1)+2=…=aM+2k,aM+5k=aM+5(k-1)+5=…=aM+5k,
取N=M+5,则,
所以,若k是偶数,则aN+k=aN+k;
若k是奇数,则aN+k=aN+5+(k-5)=aN+5+(k-5)=aN+5+(k-5)=aN+k,
所以,aN+k=aN+k
所以aN,aN+1,aN+2,…,aN+k,…是公差为1的等差数列.
点评 本题考查数列递推式的应用,考查充分、必要条件的判定,考查推理与论证能力,属于难题.

 阅读快车系列答案
阅读快车系列答案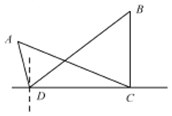 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )| A. | $20\sqrt{6}$海里 | B. | $40\sqrt{6}$海里 | C. | $20(1+\sqrt{3})$海里 | D. | 40海里 |
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
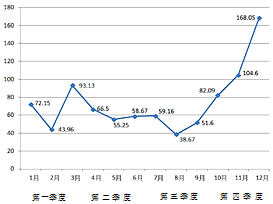 北京市2016年12个月的PM2.5平均浓度指数如图所示.由图判断,四个季度中PM2.5的平均浓度指数方差最小的是( )
北京市2016年12个月的PM2.5平均浓度指数如图所示.由图判断,四个季度中PM2.5的平均浓度指数方差最小的是( )| A. | 第一季度 | B. | 第二季度 | C. | 第三季度 | D. | 第四季度 |
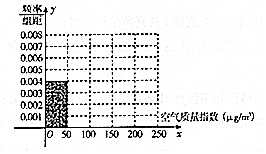 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3)区间 | [0,50) | [50,100) | [100,150) | [150,200) | [200,250) |
| 空间质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
(2)由频率分布直方图求该组数据的平均数与中位数;
(3)在空气质量指数分别属于[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件A”两天空气都为良“发生的概率.
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |