题目内容
用反证法证明命题：“三角形的三内角中至少有一个不大于60度”时，反设是“假设三角形的三内角 ．”
考点：反证法与放缩法
专题：计算题,反证法
分析：根据命题“三角形的内角中至少有一个内角不大于60°”的否定是：三角形的三个内角都大于60°，由此得到答案．
解答：
证明：用反证法证明命题：“三角形的内角中至少有一个内角不大于60°”时，
应假设命题的否定成立，而命题“三角形的内角中至少有一个内角不大于60°”的否定是：
三角形的三个内角都大于60°，
故答案为：都大于60°．
应假设命题的否定成立，而命题“三角形的内角中至少有一个内角不大于60°”的否定是：
三角形的三个内角都大于60°，
故答案为：都大于60°．
点评：本题主要考查求一个命题的否定，用反证法证明数学命题，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口，属于基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
点A、B、C、D在同一个球的球面上，且AB=CD=
，BC=2AC=2BD=2，则该球的表面积为（ ）
| 3 |
| A、16π | B、12π |
| C、8π | D、4π |
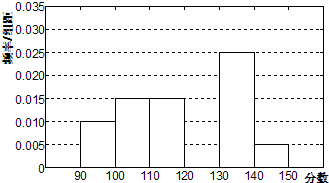武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图．观察图形的信息，回答如下问题：数列{an}的通项公式an=n2+2n，则数列{
}的前10项和为（ ）
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
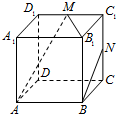如图所示，在正方体ABCD A1B1C1D1中，M、N分别是棱C1D1，C1C的中点．给出以下四个结论：