题目内容
当a≥2时，求证：
-
＜
-
．
| a+1 |
| a |
| a-1 |
| a-2 |
考点：不等式的证明
专题：证明题,分析法
分析：把证明不等式转化为寻找使不等式成立的充分条件，直到使不等式成立的充分条件显然已经具备为止．
解答：
证明：要证：
-
＜
-
，
只需证明：
+
＜
+
，
只需证明：2
•
＜2
•
，
只需证明：a2-a-2＜a2-a，
只需证明：-2＜0，显然成立，
∴
-
＜
-
．
| a+1 |
| a |
| a-1 |
| a-2 |
只需证明：
| a+1 |
| a-2 |
| a-1 |
| a |
只需证明：2
| a+1 |
| a-2 |
| a-1 |
| a |
只需证明：a2-a-2＜a2-a，
只需证明：-2＜0，显然成立，
∴
| a+1 |
| a |
| a-1 |
| a-2 |
点评：本题考查用分析法证明不等式，即证明使不等式成立的充分条件已具备．
练习册系列答案
相关题目
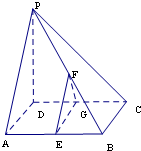如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F、G分别是AB，PB，CD的中点．
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E为PC的中点．
如图，四边形ABCD为平行四边形，四边形ADEF是正方形，且BD⊥平面CDE，H是BE的中点，G是AE，DF的交点．
如图，在四棱锥V-ABCD中，底面ABCD为正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．