题目内容

已知
a
=（1，2），
b
=（k，2）（k∈Z），
a
与
b
的夹角为
π
4
．
（1）求|
b
|
（2）求
a
•
b
．
考点：数量积表示两个向量的夹角,向量的模,平面向量数量积的运算
专题：平面向量及应用
分析：（1）由题意结合夹角公式可得k值，可得
b
=（6，2），由模长公式可得；
（2）由数量积的坐标运算可得．
解答： 解：（1）由题意可得cos
π
4
=
a
•
b
|
a
||
b
|
，
即
2
2
=
k+4
5
•
k2+4
，解得k=6，或k=-
2
3
，
∵k∈Z，∴k=6，∴
b
=（6，2）
∴|
b
|=
62+22
=2
10

（2）由（1）知
b
=（6，2），
∴
a
•
b
=1×6+2×2=10
点评：本题考查向量的模长公式和数量积，属基础题．
练习册系列答案
相关题目
已知等差数列{an}前三项的和为-3，前三项的积为8．
（1）求等差数列{an}的通项公式；
（2）若数列{an}单调递增，求数列{an}的前n项和．
已知实数a，b满足|a|＜2，|b|＜2，证明：2|a+b|＜|4+ab|．
当a≥2时，求证：
a+1
-
a
＜
a-1
-
a-2
．
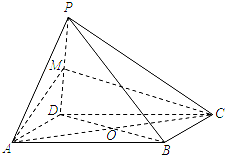如图，四棱锥P-ABCD中，O为菱形ABCD对角线的交点，M为棱PD的中点，MA=MC．
（1）求证：PB∥平面AMC；
（2）求证：平面PBD⊥平面AMC．
设关于x函数f（x）=cos2x-4acosx+2a其中0≤x≤
π
2

（1）将f（x）的最小值m表示成a的函数m=g（a）；
（2）是否存在实数a，使f（x）＞0在x∈[0，
π
2
]上恒成立？
（3）是否存在实数a，使函数f（x） 在x∈[0，
π
2
]上单调递增？若存在，写出所有的a组成的集合；若不存在，说明理由．
把一根长为30cm的木条锯成两段，分别作为钝角△ABC的两边AB和BC，且∠ABC=120°，问怎样锯断才能使第三边AC的长最短？
已知函数g（x）=x2-（2a+1）x+alnx
（Ⅰ） 当a=1时，求函数g（x）的单调增区间；
（Ⅱ） 求函数g（x）在区间[1，e]上的最小值；
（Ⅲ） 在（Ⅰ）的条件下，设f（x）=g（x）+4x-x2-2lnx，
证明：
n
k=2
1
k-f(k)
＞
3n2-n-2
n(n+1)
（n≥2）．（参考数据：ln2≈0.6931）
在三角形ABC中，D是边BC上一点，
AB
=
a
，
AC
=
b
，|
BD
|=
1
5
|
DC
|，则
AD
=
 
（用
a
，
b
表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网