题目内容
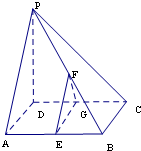如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F、G分别是AB，PB，CD的中点．（1）求证：平面EFG∥平面PAD；
（2）求证：EF⊥CD．
考点：平面与平面垂直的判定,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（1）证明EF∥平面PAD，EG∥平面PAD，利用面面平行的判定定理，可以证明平面EFG∥平面PAD；
（2）先证明EF∥PA，再证明CD⊥平面PAD，即可证明EF⊥CD．
（2）先证明EF∥PA，再证明CD⊥平面PAD，即可证明EF⊥CD．
解答：
证明：（1）E、F分别是AB、PB的中点，
∴EF∥PA．
∵EF?平面PAD，PA?平面PAD，
∴EF∥平面PAD，
同理证明EG∥平面PAD，
∵EF∩EG=E，
∴平面EFG∥平面PAD；
（2）∵E、F分别是AB、PB的中点，
∴EF∥PA．
∵ABCD是正方形，
∴AD⊥CD．
又PD⊥底面ABCD，
∴AD是斜线PA在平面ABCD内的射影．
∴PA⊥CD．
∴EF⊥CD．
∴EF∥PA．
∵EF?平面PAD，PA?平面PAD，
∴EF∥平面PAD，
同理证明EG∥平面PAD，
∵EF∩EG=E，
∴平面EFG∥平面PAD；
（2）∵E、F分别是AB、PB的中点，
∴EF∥PA．
∵ABCD是正方形，
∴AD⊥CD．
又PD⊥底面ABCD，
∴AD是斜线PA在平面ABCD内的射影．
∴PA⊥CD．
∴EF⊥CD．
点评：垂直、平行问题的证明，其一般规律是“由已知想性质，由求证想判定”，也就是说，根据已知条件去思考有关的性质定理；根据要求证的结论去思考有关的判定定理，往往需要将分析与综合的思路结合起来．
练习册系列答案
相关题目
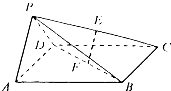如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，PA⊥PD，E、F分别为PC、BD的中点．
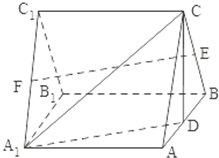如图，三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．