��Ŀ����
6����ʯͷ���������������ֳơ��¶��ǡ�����һ����������IJ�ȭ��Ϸ����Դ���й���Ȼ���ձ������ʵȵأ�������ŷó�IJ��Ϸ�չ����������ŷ�ޣ����˽����������磮����Ϸ�����ǣ���ȭ֮ǰ˫���뺰���Ȼ���ڻ�������ʱͬʱ��ȭ���ս���ȭͷ������ʯͷ����ʳָ����ָ�������������������ָ�쿪��������������ʯͷ��ʤ������������������ʤ������������������ʤ����ʯͷ������������ȭ��ͬ����Ϊ�;֣�Сǧ�ʹ�����λͬѧ���С������ʤ�ơ��ġ�ʯͷ��������������Ϸ��������Сǧ�ʹ�����������ľ�Сǧʤ���ĸ����ǣ�������| A�� | $\frac{1}{27}$ | B�� | $\frac{2}{27}$ | C�� | $\frac{2}{81}$ | D�� | $\frac{8}{81}$ |
���� Сǧ�ʹ�����������ľ�Сǧʤ������ָǰ3����Сǧʤ2�֣���1�ֲ�ʤ�����ľ�Сǧʤ���ɴ������Сǧ�ʹ�����������ľ�Сǧʤ���ĸ��ʣ�
��� �⣺���ݡ�ʯͷ��ʤ������������������ʤ������������������ʤ��ʯͷ����
�ɵ�ÿ�ֱ�����Сǧʤ���ꡢСǧ�����;ֺ�Сǧ�������ĸ��ʶ�Ϊ$\frac{1}{3}$��
��Сǧ�ʹ�����λͬѧ���С������ʤ�ơ��ġ�ʯͷ��������������Ϸ������
��Сǧ�ʹ�����������ľ�Сǧʤ������ָǰ3����Сǧʤ2�֣���1�ֲ�ʤ�����ľ�Сǧʤ��
��Сǧ�ʹ�����������ľ�Сǧʤ���ĸ����ǣ�
p=${C}_{3}^{2}��\frac{1}{3}��^{2}��\frac{2}{3}����\frac{1}{3}$=$\frac{2}{27}$��
��ѡ��B��
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע��n�ζ����ظ��������¼�Aǡ�÷���k�εĸ��ʼ��㹫ʽ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
17�������ߵļ����귽�̦�=8sin�Ȼ�Ϊֱ�����귽��ʽ��������
| A�� | x2+y2=4 | B�� | x2+��y-4��2=16 | C�� | x2+y2=1 | D�� | y=2x2 |
15���躯��f��x���Ƕ����ڣ�0��+�ޣ��ϵĿɵ��������䵼����Ϊf�䣨x����f��x����0�����������2f��x����xf�䣨x��+x����x��0ʱ�����в��ȹ�ϵһ����ȷ���ǣ�������
| A�� | 4xf��x2����x4f��2x�� | B�� | e2xf��$\frac{1}{x}$����$\frac{1}{{x}^{2}}$f��ex�� | ||
| C�� | xf��$\sqrt{x}$����f��x�� | D�� | 4xf��x+1���ܣ�x2+2x+1��f��2$\sqrt{x}$�� |
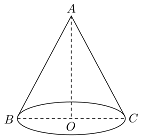 ��֪Բ�IJ���չ��ͼ��һ����Բ��
��֪Բ�IJ���չ��ͼ��һ����Բ��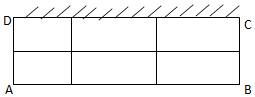 ij����������һ�䱳�濿ǽ�ij�������Ȧ����֪��Ȧ�������Ϊ18ƽ���ף�����Ȧ�ָ�ɣ���ͼ��ʾ������С��Ȧ����Ȧ�߶�Ϊ1�ף���Ȧÿƽ�������Ϊ500Ԫ���Ҳ�����Ȧ����͵���ķ�������Ȧ�ĺ�ȣ�����������������ͣ��������Ƕ��٣�
ij����������һ�䱳�濿ǽ�ij�������Ȧ����֪��Ȧ�������Ϊ18ƽ���ף�����Ȧ�ָ�ɣ���ͼ��ʾ������С��Ȧ����Ȧ�߶�Ϊ1�ף���Ȧÿƽ�������Ϊ500Ԫ���Ҳ�����Ȧ����͵���ķ�������Ȧ�ĺ�ȣ�����������������ͣ��������Ƕ��٣�