题目内容
18．在边长为2的正方形ABCD中，$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}$，点F在线段AB上运动，则$\overrightarrow{FD}•\overrightarrow{FE}$的最大值为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 先建立坐标系，再根据向量的坐标运算和向量的数量积得到$\overrightarrow{FD}•\overrightarrow{FE}$=（x+1）2+1，根据二次函数的性质即可求出最值
解答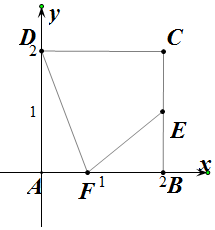 
解：以A为原点，以AB，AD所在的直线为x，y轴，建立如图所示的坐标系，
则A（0，0），B（2，0），D（0，2），C（2，2），
∵$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}$，
∴E（2，1），
∵点F在线段AB上运动，不妨设F（x，0），0≤x≤2，
∴$\overrightarrow{FD}$=（x，-2），$\overrightarrow{FE}$=（x-2，-1），
∴$\overrightarrow{FD}•\overrightarrow{FE}$=x（x-2）+2=x2-2x+2=（x+1）2+1，
当x=0时，有最大值，最大值为2，
故选：B．
点评 本题考查了向量的坐标运算和向量的数量积以及二次函数的性质，属于基础题．
练习册系列答案
相关题目
6．“石头、剪刀、布”，又称“猜丁壳”，是一种流传多年的猜拳游戏，起源于中国，然后传到日本、朝鲜等地，随着亚欧贸易的不断发展，它传到了欧洲，到了近代逐渐风靡世界．其游戏规则是：出拳之前双方齐喊口令，然后在话音刚落时同时出拳，握紧的拳头代表“石头”，食指和中指伸出代表“剪刀”，五指伸开代表“布”．“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”．若所出的拳相同，则为和局．小千和大年两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛，则小千和大年比赛至第四局小千胜出的概率是（ ）
| A． | $\frac{1}{27}$ | B． | $\frac{2}{27}$ | C． | $\frac{2}{81}$ | D． | $\frac{8}{81}$ |
13．设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P（x，y），（点P与点A，B不重合），则△PAB的面积最大值是（ ）
| A． | $2\sqrt{5}$ | B． | 5 | C． | $\frac{5}{2}$ | D． | $\sqrt{5}$ |
3．已知函数f（x）=-2tan（2x+φ）（|φ|＜π），若$f（\frac{π}{16}）=-2$，则f（x）的一个单调递减区间是（ ）
| A． | $（\frac{3π}{16}，\frac{11π}{16}）$ | B． | $（\frac{π}{16}，\frac{9π}{16}）$ | C． | $（-\frac{3π}{16}，\frac{5π}{16}）$ | D． | $（\frac{π}{16}，\frac{5π}{16}）$ |
8．下表数据为某地区某基地某种农产品的年产量x（单位：吨）及对应销售价格y（单位：万元/吨）．
（1）若y与x有较强的线性相关关系，请用最小二乘法求出y关与x的线性回归方程$\widehaty=\widehatbx+\widehata$；
（2）若每吨该农产品的成本为1万元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润z最大？最大利润是多少？
参考公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{（{{x_i}{y_i}}）}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
| x | 1 | 2 | 3 |
| y | 5 | 4 | 3 |
（2）若每吨该农产品的成本为1万元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润z最大？最大利润是多少？
参考公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{（{{x_i}{y_i}}）}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．