题目内容
设不等式组
表示的平面区域为D,在区域D内随机取一个点,则此点到直线x-5=0的距离大于7的概率是 .
|
考点:几何概型
专题:概率与统计
分析:作出可行域,以面积为测度,可得概率.
解答:
 解:如图,不等式对应的区域为△DEF及其内部.
解:如图,不等式对应的区域为△DEF及其内部.
其中D(-6,-2),E(4,-2),F(4,3),
求得直线DF、EF分别交x轴于点B(-2,0),
∵当点D在线段x=-2上时,点D到直线x-5=0的距离等于7,
∴要使点D到直线的距离大于2,则点D应在△BCD中(或其边界)
因此,根据几何概型计算公式,可得所求概率
=
.
故答案为:
.
 解:如图,不等式对应的区域为△DEF及其内部.
解:如图,不等式对应的区域为△DEF及其内部.其中D(-6,-2),E(4,-2),F(4,3),
求得直线DF、EF分别交x轴于点B(-2,0),
∵当点D在线段x=-2上时,点D到直线x-5=0的距离等于7,
∴要使点D到直线的距离大于2,则点D应在△BCD中(或其边界)
因此,根据几何概型计算公式,可得所求概率
| ||
|
| 4 |
| 25 |
故答案为:
| 4 |
| 25 |
点评:本题考查几何概型,考查面积的计算,确定以面积为测度是关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
函数g(x)=lnx-
的零点所在区间是( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
 如图,向量
如图,向量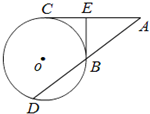 (几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=
(几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB= 如图,已知椭圆
如图,已知椭圆