题目内容
7.设向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{2π}{3}$的单位向量,若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$.分析 根据平面向量的线性运算,求出$\overrightarrow{a}$+$\overrightarrow{b}$,再利用数量积求模长.
解答 解:向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{2π}{3}$的单位向量,
且$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{a}$+$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$;
∴${(\overrightarrow{a}+\overrightarrow{b})}^{2}$=${4\overrightarrow{{e}_{1}}}^{2}$+4$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$+${\overrightarrow{{e}_{2}}}^{2}$
=4×12+4×1×1×cos$\frac{2π}{3}$+12
=3,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了平面向量的线性运算与数量积的应用问题,是基础题目.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.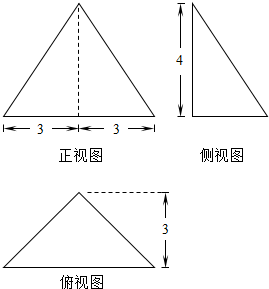 如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
 如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
如图是某个四面体的三视图,则该四面体的外接球的表面积为( )| A. | 52π | B. | 4$\sqrt{13}$π | C. | 13π | D. | $\frac{52}{3}$$\sqrt{13}$π |
18.设全集U={x∈N|-2≤x≤7},集合A={1,2,4,5},B={1,2,3,7},则∁UA∩B=( )
| A. | {1,2,3} | B. | {0,3,7} | C. | {3,7} | D. | {1,3,7} |