题目内容
10.如图,四棱锥P-ABCD的底面是边长是I的正方形,侧棱PD⊥平面ABCD,M、N分别是AB、PC的中点(1)求证:MN∥平面PAD
(2)若MN=3,求四棱锥P-ABCD的体积
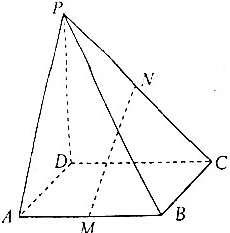
分析 (1)取CD中点Q,连结MQ,NQ.根据正方形的性质和中位线定理得出NQ∥平面PAD,NQ∥平面PAD,从而平面MNQ∥平面PAD,于是MN∥平面PAD.
(2)根据勾股定理求出NQ的长,于是PD=2NQ,代入体积公式计算.
解答  证明:(1)取CD中点Q,连结MQ,NQ.则NQ是△PCD的中位线,
证明:(1)取CD中点Q,连结MQ,NQ.则NQ是△PCD的中位线,
∴NQ∥PD,∵NQ?平面PAD,PD?平面PAD,
∴NQ∥平面PAD,
∵M是AB中点,Q是CD中点,
∴MQ∥AD,∵NQ?平面PAD,AD?平面PAD,
∴NQ∥平面PAD,
又∵NQ?平面MNQ,MQ?平面MNQ,MQ∩NQ=Q,
∴平面MNQ∥平面PAD,∵MN?平面MNQ,
∴MN∥平面PAD.
(2)∵PD⊥平面ABCD,NQ∥PD,
∴NQ⊥平面ABCD,∵MQ?平面ABCD,
∴NQ⊥MQ,又∵MQ=AD=1,∴NQ=$\sqrt{M{N}^{2}-M{Q}^{2}}$=2$\sqrt{2}$.
∴PD=2NQ=4$\sqrt{2}$.
∴V棱锥P-ABCD=$\frac{1}{3}{S}_{正方形ABCD}$•PD=$\frac{1}{3}×1×1×4\sqrt{2}$=$\frac{4\sqrt{2}}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,是中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.已知函数f(x)=x3+kx(k∈R),若关于x的方程f(x)=lnx+2ex2有唯一解,则下列说法正确的是( )
| A. | k=$\frac{1}{e}$+e | |
| B. | 函数f(x)的图象在点(0,f(0))处的切线的斜率为e2-$\frac{1}{e}$ | |
| C. | 函数f(x)在[0,e]上单调递减 | |
| D. | 函数f(x)在[0,e]上的最大值为2e3+1 |
19.已知F1、F2为双曲线的左、右焦点,P为双曲线左支上任意一点,以P为圆心,|PF1|为半径的圆与以F2为圆心,$\frac{1}{2}$|F1F2|为半径的圆相切,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
20.若复数z=$\frac{2-i}{i^3}$(i是虚数单位),则z的共轭复数为( )
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
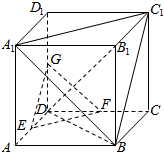 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.