题目内容
17.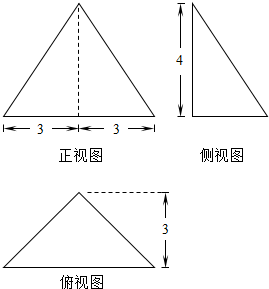 如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
如图是某个四面体的三视图,则该四面体的外接球的表面积为( )| A. | 52π | B. | 4$\sqrt{13}$π | C. | 13π | D. | $\frac{52}{3}$$\sqrt{13}$π |
分析 通过三视图,判断几何体的形状,利用三视图的数据,求出外接球的表面积,可得答案.
解答 解:由题意可知,几何体是三棱锥,
底面等腰直角三角形的底边长为6,底面三角形的高为:3,
棱锥的一条侧棱垂直底面的三角形的一个顶点,棱锥的高为:4.
其外接球相当于一个长宽高分别为:4,3$\sqrt{2}$,3$\sqrt{2}$的长方体,
故外接球的半径R满足:2R=$\sqrt{{4}^{2}+(3\sqrt{2})^{2}+(3\sqrt{2})^{2}}$=2$\sqrt{13}$,
∴外接球的表面积S=4πR2=52π,
故选:A.
点评 本题考查的知识点是由三视图求体积和表面积,球的表面积公式,根据已知,求出球的直径(半径)是解答的关键.

练习册系列答案
相关题目
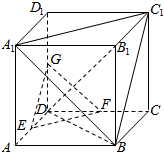 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.