题目内容
4.计算下列各式:(1)已知tanα=2,求$\frac{cosα+sinα}{cosα-sinα}$值;
(2)化简f(α)=$\frac{{sin(α-\frac{π}{2})cos(\frac{π}{2}-α)tan(π-α)}}{tan(π+α)sin(π+α)}$.
分析 (1)利用已知条件以及同角三角函数的基本关系求得$\frac{cosα+sinα}{cosα-sinα}$值.
(2)利用诱导公式求得要求式子的值.
解答 解:(1)∵已知tanα=2,∴$\frac{cosα+sinα}{cosα-sinα}$=$\frac{1+tanα}{1-tanα}$=$\frac{1+2}{1-2}=-3$.
(2)f(α)=$\frac{{sin(α-\frac{π}{2})cos(\frac{π}{2}-α)tan(π-α)}}{tan(π+α)sin(π+α)}$=$\frac{{-sin(\frac{π}{2}-α)•sinα•(-tanα)}}{tanα•(-sinα)}$=$-sin(\frac{π}{2}-α)$=-cosα.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)=aln(x+1)-x2,若对?p,q∈(0,1),且p≠q,有$\frac{{f({p+1})-f({q+1})}}{p-q}>2$恒成立,则实数a的取值范围为( )
| A. | (-∞,18) | B. | (-∞,18] | C. | [18,+∞) | D. | (18,+∞) |
8.某几何体的三视图如图所示,则其体积为( )
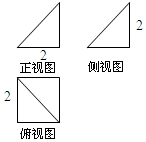

| A. | 4 | B. | $\frac{7}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
12.已知向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(-1,1),$\overrightarrow{c}$=(2,3),若$\overrightarrow{a}$+λ$\overrightarrow{b}$与$\overrightarrow{c}$共线,则实数λ=( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |