题目内容
16．已知函数f（x）=$\frac{{e}^{x}}{x}$-alnx-$\frac{a}{x}$（a∈R）．（1）当a=1时，求f（x）在（1，f（1））处的切线方程；
（2）当x＞1时，f（x）＞e-a，求实数a的取值范围．
分析 （1）求导数，确定切线的斜率，即可求f（x）在（1，f（1））处的切线方程；
（2）当x＞1时，f（x）＞e-a，求导数，分类讨论，即可求实数a的取值范围．
解答 解：（1）当a=1时，f′（x）=$\frac{（{e}^{x}-1）（x-1）}{{x}^{2}}$，f（1）=e-1，f′（1）=0，
∴f（x）在（1，f（1））处的切线方程为y=e-1；
（2）f′（x）=$\frac{（{e}^{x}-1）（x-a）}{{x}^{2}}$，
a≤1，函数在（0，+∞）上单调递增，∵f（x）＞e-a，∴f（x）＞f（1）=e-a，成立；
a＞1时，函数在（1，a）上单调递减，（a，+∞）上单调递增，x=a时，函数取得最小值，
∵f（x）＞e-a，∴$\frac{{e}^{a}}{a}-alna-1＞e-a$，不成立，
综上所述，a≤1．
点评 本题考查导数知识的综合运用，考查导数的几何意义，考查函数的单调性，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
19．
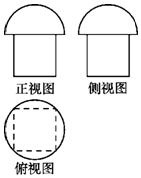一个几何体的三视图如图所示，其中正视图和侧视图相同，其上部分是半圆，下部分是边长为2的正方形；俯视图是边长为2的正方形及其外接圆．则该几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图和侧视图相同，其上部分是半圆，下部分是边长为2的正方形；俯视图是边长为2的正方形及其外接圆．则该几何体的体积为（ ）| A． | $4+\frac{2π}{3}$ | B． | $4+\frac{{2\sqrt{2}π}}{3}$ | C． | $8+\frac{{4\sqrt{2}π}}{3}$ | D． | $8+\frac{{8\sqrt{2}π}}{3}$ |
20．若函数$f（x）=\left\{\begin{array}{l}cosx，x≤a\\ \frac{1}{x}，x＞a\end{array}\right.$的值域为[-1，1]，则实数a的取值范围是（ ）
| A． | [1，+∞） | B． | （-∞，-1] | C． | （0，1] | D． | （-1，0） |
8．已知M为平面内一动点，设命题甲：存在两个定点F1，F2使得||MF1|-|MF2||是定值，命题乙：M的轨迹是双曲线，则命题甲是命题乙的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |