题目内容
9.等差数列{an}和等比数列{bn}中,Sn为数列{an}的前n项和,Tn为数列{bn}的前n项和,若a1=2,S3=12,T2=3,T4=15(1)求a6;
(2)求T6.
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)利用等比数列的通项公式与求和公式即可得出.
解答 解:(1)设数列{an}的公差为d,由题意可知${S_3}=3{a_1}+\frac{3×2}{2}d$,代入数据解之得,d=2,(3分)
由等差数列通项公式an=a1+(n-1)d,可得a6=2+2×5=12.(3分).
(2)设等比数列{bn}的公比为q,首项为b1.由题意可知$\left\{{\begin{array}{l}{{T_2}=\frac{{{b_1}(1-{q^2})}}{1-q}}\\{{T_4}=\frac{{{b_1}(1-{q^4})}}{1-q}}\end{array}}\right.$,
代入数据解之得q=2,b1=1或q=-2,b1=-3(3分),
∴q=2,b1=1时,T6=$\frac{{2}^{6}-1}{2-1}$=63;
q=-2,b1=-3时,T6=$\frac{-3[1-(-2)^{6}]}{1-(-2)}$=63.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
12.某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ,求随机变量ξ的分布列及数学期望.
| 班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
| 频数 | 5 | 9 | 11 | 9 | 7 | 9 |
| 满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ,求随机变量ξ的分布列及数学期望.
18.圆的一条直径的两个端点是(2,0),(0,2)时,则此圆的方程是( )
| A. | (x-2)2+(y-1)2=1 | B. | (x-1)2+(y-1)2=2 | C. | (x-1)2+(y+1)2=9 | D. | (x+2)2+(y+1)2=2 |
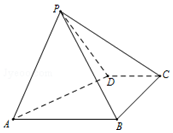 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形