题目内容
如图所示，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A作l的垂线AD，垂足为D，则线段AE的长等于考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接OC，先证得三角形OBC是等边三角形，从而得到∠DCA=60°，再在直角三角形ACD中得到∠DAC的大小；考虑到直角三角形ABE中，利用角的关系即可求得边AE的长．
解答：
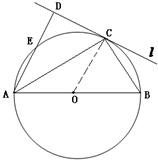解：如图，连接OC，
因为BC=OB=OC=3，
所以∠CBO=60°，
因为∠DCA=∠CBO，
所以∠DCA=60°，
又AD⊥DC得∠DAC=30°，
又因为∠ACB=90°，
得∠CAB=30°，那么∠EAB=60°，
从而∠ABE=30°，
于是AE=3．
故答案为：3．
解：如图，连接OC，因为BC=OB=OC=3，
所以∠CBO=60°，
因为∠DCA=∠CBO，
所以∠DCA=60°，
又AD⊥DC得∠DAC=30°，
又因为∠ACB=90°，
得∠CAB=30°，那么∠EAB=60°，
从而∠ABE=30°，
于是AE=3．
故答案为：3．
点评：熟练掌握圆的性质、切线的性质、等边三角形的判定、含30°角的直角三角形的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
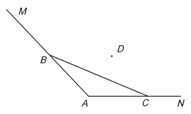在一个六角形体育馆的一角MAN内，用长为a的围栏设置一个运动器材储存区域（如图所示），已知∠A=120°，B是墙角线AM上的一点，C是墙角线AN上的一点．