题目内容
设函数f(x)是定义在(-2,2)上的奇函数,且在(-2,2)上的减函数,若函数f(x)满足:f(m-1)+f(2m-1)>0,则实数m的取值范围是 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:利用函数的奇偶性单调性即可得出.
解答:
解:∵函数f(x)是定义在(-2,2)上的奇函数,函数f(x)满足:f(m-1)+f(2m-1)>0,
∴f(m-1)>-f(2m-1)=f(1-2m),
∵函数f(x)在(-2,2)上的减函数,
∴-2<m-1<1-2m<2,
解得-
<m<
.
∴m的取值范围是-
<m<
.
故答案为:-
<m<
.
∴f(m-1)>-f(2m-1)=f(1-2m),
∵函数f(x)在(-2,2)上的减函数,
∴-2<m-1<1-2m<2,
解得-
| 1 |
| 2 |
| 2 |
| 3 |
∴m的取值范围是-
| 1 |
| 2 |
| 2 |
| 3 |
故答案为:-
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查了函数的奇偶性单调性,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
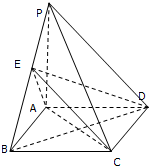 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=