题目内容
10.已知函数f(x)=2017x+log2017($\sqrt{{x}^{2}+1}$+x)-2017-x+1,则关于x的不等式f(2x+1)+f(x+1)>2的解集为( )| A. | (-$\frac{1}{2017}$,+∞) | B. | (-2017,+∞) | C. | (-$\frac{2}{3}$,+∞) | D. | (-2,+∞) |
分析 可先设g(x)=2017x+log2017($\sqrt{{x}^{2}+1}$+x)-2017-x,根据要求的不等式,可以判断g(x)的奇偶性及其单调性,容易求出g(-x)=-g(x),通过求g′(x),并判断其符号可判断其单调性,从而原不等式可变成,g(2x+1)>g(-x-1),而根据g(x)的单调性即可得到关于x的一元一次不等式,解该不等式即得原不等式的解集.
解答 解:设g(x)=2017x+log2017($\sqrt{{x}^{2}+1}$+x)-2017-x,
则g(-x)=2017-x+log2017($\sqrt{{x}^{2}+1}$-x)-2017x=-g(x),
g′(x)=2017xln2017+$\frac{1}{ln2017•\sqrt{{x}^{2}+1}}$+2017-xln2017>0,
可得g(x)在R上单调递增;
∴由f(2x+1)+f(x+1)>2得,g(2x+1)+1+g(x+1)+1>2;
∴g(2x+1)>-g(x+1),即为g(2x+1)>g(-x-1),
得2x+1>-x-1,
解得x>-$\frac{2}{3}$,
∴原不等式的解集为(-$\frac{2}{3}$,+∞).
故选:C.
点评 本题考查对数的运算,平方差公式,奇函数的判断方法,根据函数导数符号判断函数单调性的方法,函数单调性定义的运用,并注意正确求导.

练习册系列答案
相关题目
1.将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,所得函数的解析式为( )
| A. | $y=sin({2x+\frac{5π}{6}})$ | B. | y=-cos2x | C. | y=cos2x | D. | $y=sin({2x-\frac{π}{6}})$ |
5.已知双曲线$\frac{{x}^{2}}{m}$-y2=1的一个焦点与抛物线y2=8x焦点相同,则此双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{15}}{15}$ |
19.若函数f(x)=sin(x+φ)是偶函数,则φ可取一个值为( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
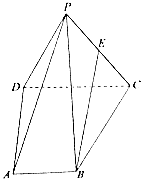 如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.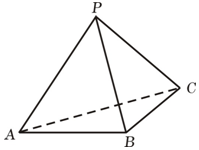 如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.
如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.