题目内容
18.已知函数f(x)=ex-$\frac{a}{x}$,a,f(x)为实数.(1)当a>0时,求函数f(x)的单调区间;
(2)若f(x)在(0,+∞)上存在极值点,且极值大于ln4+2,求a的取值范围.
分析 (1)先求导,再根据导数和函数单调性的关系即可求出答案,
(2)设极值点为x0,则极值为f(x0)=${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$,多次构造函数,利用导数和函数的最值得关系即可求出a的取值范围.
解答 解:(1)f(x)=ex-$\frac{a}{x}$的定义域为(-∞,0)∪(0,+∞),
∴f′(x)=ex+$\frac{a}{{x}^{2}}$,
∵a>0,
∴f′(x)=ex+$\frac{a}{{x}^{2}}$>0恒成立,
∴f(x)在(-∞,0),(0,+∞)上单调递增,
(2)由(1)可知,当a≥0时,f(x)在(-∞,0),(0,+∞)上单调递增,函数无极值点,
当a<0时,
∵f(x)在(0,+∞)上存在极值点,
∴f′(x)=ex+$\frac{a}{{x}^{2}}$=$\frac{{x}^{2}{e}^{x}+a}{{x}^{2}}$
设g(x)=x2ex+a,
则g′(x)=xex(2+x)>0在(0,+∞)上恒成立,
∴g(x)在(0,+∞)上单调递增,
∴g(x)>g(0)=a<0,
设极值点为x0,则极值为f(x0)=${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$,
由g(x0)=0,得a=-x02e${\;}^{{x}_{0}}$.
∴f(x0)=${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=(x0+1)e${\;}^{{x}_{0}}$.
令h(x)=(x+1)ex,
∴h′(x)=(x+2)ex,
∴h(x)在(0,+∞)上单调递增,
而f(x0)=${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=(x0+1)e${\;}^{{x}_{0}}$>ln4+2=2(ln2+1)=(ln2+1)eln2,
∴x0>ln2,
令φ(x)=-x2ex,
∴x0>ln2时吗,φ(x)=-xex(2+x)<0,
∴φ(x)单调递减,
∴a<-(ln2)2eln2=-2ln22,
∴a的取值范围为(-∞,-2ln22).
点评 本题考查函数单调性与导数间的关系及函数取得极值的条件,考查学生分析问题解决问题的能力,属于难题

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | (4,4) | B. | (2,4) | C. | (-2,4) | D. | (-4,4) |
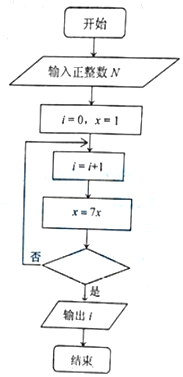 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
| A. | (-$\frac{1}{2017}$,+∞) | B. | (-2017,+∞) | C. | (-$\frac{2}{3}$,+∞) | D. | (-2,+∞) |
| A. | (-∞,$\frac{1}{5}$] | B. | [-$\frac{1}{5}$,1] | C. | (-$\frac{1}{5}$,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1] |