题目内容
1.将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,所得函数的解析式为( )| A. | $y=sin({2x+\frac{5π}{6}})$ | B. | y=-cos2x | C. | y=cos2x | D. | $y=sin({2x-\frac{π}{6}})$ |
分析 根据函数y=Asin(ωx+φ)的图象变换规律即可得解.
解答 解:将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,
所得函数的解析式为y=sin[2(x+$\frac{π}{3}$)+$\frac{π}{6}$]=sin(2x+$\frac{2π}{3}$+$\frac{π}{6}$)=sin(2x+$\frac{5π}{6}$).
故选:A.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换规律的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.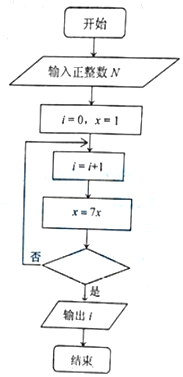 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
10.已知函数f(x)=2017x+log2017($\sqrt{{x}^{2}+1}$+x)-2017-x+1,则关于x的不等式f(2x+1)+f(x+1)>2的解集为( )
| A. | (-$\frac{1}{2017}$,+∞) | B. | (-2017,+∞) | C. | (-$\frac{2}{3}$,+∞) | D. | (-2,+∞) |
 据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.
据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.