题目内容
已知数列{an}是各项均为正数的等比数列，且a2+a4=10，a3a5=64．
（1）求数列{an}的通项公式；
（2）设bn=2nan，求数列{bn}的前n项．
（1）求数列{an}的通项公式；
（2）设bn=2nan，求数列{bn}的前n项．
考点：数列的求和,等比数列的性质
专题：等差数列与等比数列
分析：（1）利用等比数列的通项公式即可得出；
（2）利用等比数列的前n项和公式、“错位相减法”即可得出．
（2）利用等比数列的前n项和公式、“错位相减法”即可得出．
解答：
解：（1）设等比数列{an}公比为q＞0，an＞0，
∵a2+a4=10，a3a5=64．
∴
，解得
，
∴an=1×2n-1=2n-1．
（2）bn=2nan=2n•2n-1=n•2n，
∴数列{bn}的前n项Sn=2+2×22+3×23+…+n•2n，
∴2Sn=22+2×23+…+（n-1）•2n+n•2n+1，
∴-Sn=2+22+23+…+2n-n•2n+1=
-n•2n+1=（1-n）•2n+1-2，
∴Sn=（n-1）•2n+1+2．
∵a2+a4=10，a3a5=64．
∴
|
|
∴an=1×2n-1=2n-1．
（2）bn=2nan=2n•2n-1=n•2n，
∴数列{bn}的前n项Sn=2+2×22+3×23+…+n•2n，
∴2Sn=22+2×23+…+（n-1）•2n+n•2n+1，
∴-Sn=2+22+23+…+2n-n•2n+1=
| 2(2n-1) |
| 2-1 |
∴Sn=（n-1）•2n+1+2．
点评：本题考查了等比数列的通项公式与前n项和公式、“错位相减法”，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=（-1，2，4），
=（x，-1，-2），并且
⊥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
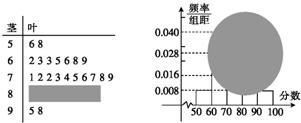某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，据此解答如下问题：