题目内容
已知C为线段AB的中点,P为直线AB外一点,满足|
|=|
|=3,|
-
|=4,
=λ
=m(
+
)+
,m>0,则λ= .
| PA |
| PB |
| PA |
| PB |
| PI |
| IC |
| BI |
| ||
|
|
| ||
|
|
| BA |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据向量的正交分解,
沿
和
方向分解,设得到两个向量为
和
,得到四边形ADIE为棱形,由棱形的性质及根据角平分线定理即可求出
| AI |
| AP |
| AC |
| AD |
| AE |
解答:
解:将
沿
和
方向分解,设得到两个向量为
和
,
∴
=m单位向量,
=m单位向量,
∵单位向量的模长为1,
∴|
|=|
|=1,
∴四边形ADIE为棱形,
∴AI平分∠PAC,
∴|
-
|=|
|=4,
∴AC=2,
根据角平分线定理,得
=
=
,
∴λ=
,
故答案为:
.
| AI |
| AP |
| AC |
| AD |
| AE |
∴
| AD |
| AE |
∵单位向量的模长为1,
∴|
| AD |
| AE |
∴四边形ADIE为棱形,
∴AI平分∠PAC,
∴|
| PA |
| PB |
| BA |
∴AC=2,
根据角平分线定理,得
| AP |
| AC |
| PI |
| IC |
| 3 |
| 2 |
∴λ=
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了向量的正交分解,以及有关四边形和角平分线的性质,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,若cosC=2sinAsinB-1,sin2A+sin2B=1,则此三角形为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
已知向量
=(-1,2,4),
=(x,-1,-2),并且
⊥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
设m,n表示不同的直线,α,β表示不同的平面,则下列命题中不正确的是( )
| A、m⊥α,n⊥α,则m∥n |
| B、m⊥α,α∥β,则m⊥β |
| C、m∥n,m⊥α,则n⊥α |
| D、m∥α,α∩β=n,则m∥n |
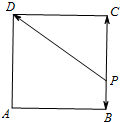 如图,正方形ABCD的边长为2,点P是线段BC上的动点,则(
如图,正方形ABCD的边长为2,点P是线段BC上的动点,则(