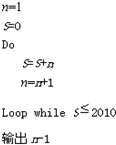题目内容
已知直线l经过两点A(2,1),B(6,3)
(1)求直线l的方程;
(2)圆C的圆心在直线l上,并且与x轴相切于点(2,0),求圆C的方程;
(3)若过B点向(2)中圆C引切线,BS、BT,S、T分别是切点,求ST直线的方程.
(1)求直线l的方程;
(2)圆C的圆心在直线l上,并且与x轴相切于点(2,0),求圆C的方程;
(3)若过B点向(2)中圆C引切线,BS、BT,S、T分别是切点,求ST直线的方程.
考点:圆的切线方程,圆的标准方程
专题:直线与圆
分析:(1)根据两点式方程即可求直线l的方程;
(2)根据直线和圆相切建立条件关系即可求圆C的方程;
(3)根据直线和圆相切建立条件关系即可求ST直线的方程.
(2)根据直线和圆相切建立条件关系即可求圆C的方程;
(3)根据直线和圆相切建立条件关系即可求ST直线的方程.
解答:
解:(1)由题可知:直线l经过点(2,1),(6,3),由两点式可得直线l的方程为:
=
整理得:x-2y=0,
(2)依题意:设圆C的方程为:(x-2)2+y2+ky=0,(k≠0)其圆心为(2,-
)
∵圆心C在x-2y=0上,
∴2-2•(-
)=0,∴k=-2.
∴圆C的方程为(x-2)2+y2-2y=0,
即(x-2)2+(y-1)2=5.
(3)圆(x-2)2+(y-1)2=5的圆心为C(2,1)
则BC的中点坐标为(4,2),|BC|=
=2
∵S、T分别是切点,
∴以B(6,3),C(2,1)为直径的圆的方程为(x-4)2+(y-2)2=5,
即x2+y2-8x-4y+15=0,
∵C的方程为x2+y2-4x-2y+4=0,
∴两个方程相减得4x+2y-11=0.
| y-1 |
| 3-1 |
| x-2 |
| 6-2 |
(2)依题意:设圆C的方程为:(x-2)2+y2+ky=0,(k≠0)其圆心为(2,-
| k |
| 2 |
∵圆心C在x-2y=0上,
∴2-2•(-
| k |
| 2 |
∴圆C的方程为(x-2)2+y2-2y=0,
即(x-2)2+(y-1)2=5.
(3)圆(x-2)2+(y-1)2=5的圆心为C(2,1)
则BC的中点坐标为(4,2),|BC|=
| 20 |
| 5 |
∵S、T分别是切点,
∴以B(6,3),C(2,1)为直径的圆的方程为(x-4)2+(y-2)2=5,
即x2+y2-8x-4y+15=0,
∵C的方程为x2+y2-4x-2y+4=0,
∴两个方程相减得4x+2y-11=0.
点评:本题主要考查圆的方程的求解,以及圆的相交弦的求解,考查学生的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过点M(0,1)与抛物线y2=2x只有一个公共点的直线有( )
| A、1条 | B、2条 | C、3条 | D、0条 |
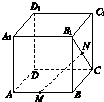 如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设
如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| MN |
| a |
| b |
| c |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
不等式(x-1)(x-2)(x-3)>0的解集是( )
| A、(1,2) |
| B、(1,2)∪(3,+∞) |
| C、(1,3) |
| D、(2,3) |