题目内容

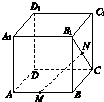如图，在正方体ABCD-A1B1C1D1中，M、N分别为AB、B1C的中点，设
AB
=
a
，
AD
=
b
，
AA1
=
c
，若
MN
=x
a
+y
b
+z
c
，则（　　）
A、x=
1
2
，y=
1
3
，z=
1
4
B、x=
1
2
，y=
1
2
，z=1
C、x=
1
2
，y=
1
2
，z=
1
2
D、x=
1
2
，y=
1
2
，z=3
考点：空间向量运算的坐标表示
专题：
分析：利用向量的多边形法则、向量相等即可得出．
解答： 解：∵
MN
=
MB
+
BC
+
CN

=
1
2
AB
+
AD
+
1
2
(
CB
+
BB1
)
=
1
2
AB
+
AD
+
1
2
(-
AD
+
AA1
)
=
1
2
AB
+
1
2
AD
+
1
2
AA1
．
又
MN
=x
a
+y
b
+z
c
，故有x=
1
2
，y=
1
2
，z=
1
2
，
故选C．
点评：熟练掌握向量的多边形法则、向量相等是解题的关键
练习册系列答案
相关题目
在空间内，可以确定一个平面的条件是（　　）
A、三条直线，它们两两相交，但不交于同一点
B、三条直线，其中的一条与另外两条直线分别相交
C、三个点
D、两两相交的三条直线
已知函数f（x）的图象如图所示，若函数y=f（x）-
1
x
-a在区间[-10，10]上有10个零点（互不相同），则实数a的取值范围是（　　）
A、[-
4
5
，
4
5
]
B、(-
4
5
，
4
5
)
C、[-
1
10
，
1
10
]
D、(-
1
10
，
1
10
)
已知函数f（x）=|sinx|+|cosx|-sin2x-1（x∈R），则下列命题正确的是
 
（写出所有正确命题的序号）．
①f（x）是周期函数；
②f（x）的图象关于x=
π
2
对称；
③f（x）的最小值为
2
-2；
④f（x）的单调递减区间为[kπ+
π
4
，kπ+
3π
4
]（k∈Z）；
⑤f（x）在（0，nπ）内恰有2015个零点，则n的取值范围为1.007.5＜n＜1008．
已知函数f（x）=x3-3a2x2-2ax，x∈[0，1]，且a≥1．
（Ⅰ）判断函数f（x）的单调性并予以证明；
（Ⅱ）若函数f（x）的值域为A，且[-4，-3]⊆A，求实数a的取值范围．
已知函数f（x）=（a+1）lnx+x2-x （a∈R），
（Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）设a＞0，如果对任意x1，x2∈（0，+∞），均有f（x1）-f（x2）＞3|x1-x2|，求a的取值范围．
设P（x，y）是椭圆
x2
9
+
y2
4
=1上的一点，则2x-y的最大值是
 
．
已知直线l经过两点A（2，1），B（6，3）
（1）求直线l的方程；
（2）圆C的圆心在直线l上，并且与x轴相切于点（2，0），求圆C的方程；
（3）若过B点向（2）中圆C引切线，BS、BT，S、T分别是切点，求ST直线的方程．
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且
3
a=2csinA
（1）确定角C的大小；
（2）若c=
7
，且△ABC的面积为
3
3
2
，求a+b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网