题目内容
过点M(0,1)与抛物线y2=2x只有一个公共点的直线有( )
| A、1条 | B、2条 | C、3条 | D、0条 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意画出图象,然后分斜率为0,斜率不存在,斜率存在不为0分析求解.
解答:
解:如图,
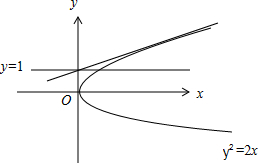
当过点M(0,1)的直线斜率为0或斜率不存在时,直线与抛物线y2=2x只有一个公共点,
直线方程分别为y=1,x=0;
当直线的斜率存在且不为0时,设为k,
则直线方程的斜截式为y=kx+1,
联立
,得k2x2+(2k-2)x+1=0.
由△=(2k-2)2-4k2=0,得k=
.
直线方程为y=
x+1.
∴过点M(0,1)与抛物线y2=2x只有一个公共点的直线有3条.
故选:C.

当过点M(0,1)的直线斜率为0或斜率不存在时,直线与抛物线y2=2x只有一个公共点,
直线方程分别为y=1,x=0;
当直线的斜率存在且不为0时,设为k,
则直线方程的斜截式为y=kx+1,
联立
|
由△=(2k-2)2-4k2=0,得k=
| 1 |
| 2 |
直线方程为y=
| 1 |
| 2 |
∴过点M(0,1)与抛物线y2=2x只有一个公共点的直线有3条.
故选:C.
点评:本题考查了抛物线的简单几何性质,考查了分类讨论的数学思想方法,是中档题,也是易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在空间内,可以确定一个平面的条件是( )
| A、三条直线,它们两两相交,但不交于同一点 |
| B、三条直线,其中的一条与另外两条直线分别相交 |
| C、三个点 |
| D、两两相交的三条直线 |
已知M(x0,y0)是圆x2+y2=r2(r>0)内异于圆心的一点,则此直线x0x+y0y=r2与该圆( )
| A、相交 | B、相切 | C、相离 | D、不确定 |
已知函数f(x)的图象如图所示,若函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),则实数a的取值范围是( )

| 1 |
| x |

A、[-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-
|