题目内容
已知正三角形OEF的三个顶点(O为坐标原点)都在抛物线上x2=y,圆D为三角形OEF的外接圆.圆C的方程为(x-5cosα)2+(y-5sinα-2)2=1(a∈R),过圆C上任意一点M作圆D的两条切线MA,MB,切点分别为A,B,设d=|MA|.
(Ⅰ)求圆D的方程;
(Ⅱ)试用d表示
•
,并求
•
的最小值.
(Ⅰ)求圆D的方程;
(Ⅱ)试用d表示
| MA |
| MB |
| MA |
| MB |
考点:圆的标准方程,平面向量数量积的运算
专题:直线与圆
分析:(Ⅰ)设E(x1,x12),F(x2,x22),x1>x2,由已知得E(
,3),F(-
,3),由此能求出圆D的方程.
(Ⅱ)圆心C(5cosα,5sinα+2),从而|DC|=5,由圆的向何性质,得4≤|DM|≤6,2
≤d≤4
,由此能求出
•
取得最小值为6.
| 3 |
| 3 |
(Ⅱ)圆心C(5cosα,5sinα+2),从而|DC|=5,由圆的向何性质,得4≤|DM|≤6,2
| 3 |
| 2 |
| MA |
| MB |
解答:
解:(Ⅰ)设E(x1,x12),F(x2,x22),x1>x2,
∵△OEF是正三角形,∴
×
=x12,
解得x1=
,则E(
,3),
同理,F(-
,3),
∴外接圆的圆心为(0,2),半径为2,
故圆D的方程为x2+(y-2)2=4.
(Ⅱ)圆心C(5cosα,5sinα+2),
∴|DC|=5,
由圆的几何性质,得:
|DC|-1≤|DM|≤|DC|+1,即4≤|DM|≤6,
又|DA|=2,在Rt△DAM中,由勾股定理,得:
d=|MA|=
=
,
∴2
≤d≤4
,
设∠DMA=θ,则tanθ=
=
,
∴cos∠AMB=cos2θ=cos2θ-sin2θ
=
=
=
,
∴
•
=|
|•|
|cos∠AMB=d2•
,
令t=d2+4,则t∈[16,36],
∴
•
=
=t+
-12,
令f(t)=t+
-12,t∈[16,36],
则f′(t)=1-
=
>0,
∴f(t)在[16,36]上单调递增,
当t=d2+4=16,即d=2
时,
•
取得最小值为6.
∵△OEF是正三角形,∴
| ||
| 2 |
| (x1)2+(x12)2 |
解得x1=
| 3 |
| 3 |
同理,F(-
| 3 |
∴外接圆的圆心为(0,2),半径为2,
故圆D的方程为x2+(y-2)2=4.
(Ⅱ)圆心C(5cosα,5sinα+2),
∴|DC|=5,
由圆的几何性质,得:
|DC|-1≤|DM|≤|DC|+1,即4≤|DM|≤6,
又|DA|=2,在Rt△DAM中,由勾股定理,得:
d=|MA|=
| |DM|2-|DA|2 |
| |DM|2-4 |
∴2
| 3 |
| 2 |
设∠DMA=θ,则tanθ=
| |DA| |
| |MA| |
| 2 |
| d |
∴cos∠AMB=cos2θ=cos2θ-sin2θ
=
| cos2θ-sin2θ |
| cos2θ+sin2θ |
=
| 1-tan2θ |
| 1+tan2θ |
| d2-4 |
| d2+4 |
∴
| MA |
| MB |
| MA |
| MB |
| d2-4 |
| d2+4 |
令t=d2+4,则t∈[16,36],
∴
| MA |
| MB |
| (t-4)(t-8) |
| t |
| 32 |
| t |
令f(t)=t+
| 32 |
| t |
则f′(t)=1-
| 32 |
| t2 |
| t2-32 |
| t2 |
∴f(t)在[16,36]上单调递增,
当t=d2+4=16,即d=2
| 3 |
| MA |
| MB |
点评:本题考查圆D的方程的求法,考查
•
的最小值的求法,是中档题,解题时要注意圆的性质的合理运用.
| MA |
| MB |

练习册系列答案
相关题目
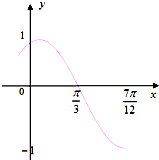 函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
如图所示的程序框图中,输入x=2,则输出的结果是( )


| A、1 | B、2 | C、3 | D、4 |