题目内容
已知椭圆:
+y2=1,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A、B两点.
(Ⅰ)求证O到直线AB的距离为定值;
(Ⅱ)求△OAB面积的最大值.
| x2 |
| 3 |
(Ⅰ)求证O到直线AB的距离为定值;
(Ⅱ)求△OAB面积的最大值.
考点:椭圆的简单性质
专题:计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设A(x1,y1),B(x2,y2),若k存在,则设直线AB:y=kx+m,联立椭圆方程,消去y,运用韦达定理,由OA⊥OB,则有x1x2+y1y2=0,化简整理,再由点到直线的距离,即可得到定值;若AB的斜率不存在时,显然成立;
(Ⅱ)运用弦长公式,化简整理,再由基本不等式,即可得到最大值,当斜率不存在时,经检验|AB|<2也成立,则有△OAB面积的最大值.
(Ⅱ)运用弦长公式,化简整理,再由基本不等式,即可得到最大值,当斜率不存在时,经检验|AB|<2也成立,则有△OAB面积的最大值.
解答:
(Ⅰ)证明:设A(x1,y1),B(x2,y2),
若k存在,则设直线AB:y=kx+m.
由
,得
(1+3k2)x2+6kmx+3m2-3=0,
则x1+x2=-
,x1x2=
,①
由OA⊥OB,
知x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
将①代入,得4m2=3k2+3,即有m2=
(k2+1),
则有原点到直线AB的距离d=
=
,
当AB的斜率不存在时,|x1|=|y1|,可得|x1|=
=d,依然成立.
所以点O到直线AB的距离为定值
.
(Ⅱ)解:|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
)2-4×
]
=
=3+
=3+
≤3+
=4,
当且仅当9k2=
,即k=±
时等号成立.
当斜率不存在时,经检验|AB|<2.
所以S△OAB≤
×2×
=
,
即有△OAB面积的最大值为
.
若k存在,则设直线AB:y=kx+m.
由
|
(1+3k2)x2+6kmx+3m2-3=0,
则x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
由OA⊥OB,
知x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
将①代入,得4m2=3k2+3,即有m2=
| 3 |
| 4 |
则有原点到直线AB的距离d=
| |m| | ||
|
| ||
| 2 |
当AB的斜率不存在时,|x1|=|y1|,可得|x1|=
| ||
| 2 |
所以点O到直线AB的距离为定值
| ||
| 2 |
(Ⅱ)解:|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
=
| 3(9k4+10k2+1) |
| 9k4+6k2+1 |
| 12k2 |
| 9k4+6k2+1 |
| 12 | ||
9k2+
|
≤3+
| 12 |
| 6+6 |
当且仅当9k2=
| 1 |
| k2 |
| ||
| 3 |
当斜率不存在时,经检验|AB|<2.
所以S△OAB≤
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
即有△OAB面积的最大值为
| ||
| 2 |
点评:本题考查椭圆的方程和运用,考查直线方程和椭圆方程联立,消去未知数,运用韦达定理和弦长公式,考查点到直线的距离公式和基本不等式的运用,属于中档题.

练习册系列答案
相关题目
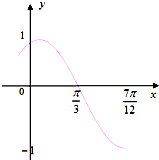 函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
