题目内容
直线
+
=1（a＞0，b＞0）经过点（1，1），则ab的最小值为 ．
| x |
| a |
| y |
| b |
考点：直线的截距式方程
专题：不等式的解法及应用
分析：根据题意，将点（1，1）代入直线
+
=1，可得
+
=1，再利用基本不等式即可求出ab的最小值．
| x |
| a |
| y |
| b |
| 1 |
| a |
| 1 |
| b |
解答：
解：∵直线
+
=1（a＞0，b＞0）经过点（1，1），
∴
+
=1．
又∵a＞0，b＞0时，由基本不等式可得
+
≥2
．
∴
≤
．
∴ab≥4．此时，a=b=2．
∴ab的最小值为4．
故答案为：4
| x |
| a |
| y |
| b |
∴
| 1 |
| a |
| 1 |
| b |
又∵a＞0，b＞0时，由基本不等式可得
| 1 |
| a |
| 1 |
| b |
|
∴
| 1 |
| ab |
| 1 |
| 4 |
∴ab≥4．此时，a=b=2．
∴ab的最小值为4．
故答案为：4
点评：本题考查直线的截距式方程，基本不等式等知识的综合应用，属于中档题．
练习册系列答案
相关题目
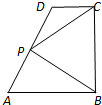如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设
某几何体的三视图如图所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成，则该几何体的体积为（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|