题目内容
已知椭圆C的方程为
+
=1(a>b>0),左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足∠F1MF2=60°,且S△F1MF2=
(1)求椭圆C的方程;
(2)过点P(0,2)分别作直线PA、PB交椭圆C于A、B两点,设PA、PB的斜率分别是k1,k2,且k1+k2=4,求证:直线AB过定点,并求出直线AB的斜率k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
4
| ||
| 3 |
(1)求椭圆C的方程;
(2)过点P(0,2)分别作直线PA、PB交椭圆C于A、B两点,设PA、PB的斜率分别是k1,k2,且k1+k2=4,求证:直线AB过定点,并求出直线AB的斜率k的取值范围.
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设|MF1|=m,|MF2|=n,利用余弦定理,结合三角形的面积公式,可求a,结合c,可求b,即可求椭圆C的方程;
(2)设直线AB的方程为y=kx+m,代入椭圆方程,利用韦达定理,结合k1+k2=4,可得m=k-2,即可证明直线AB过定点,利用△≥0,求出直线AB的斜率k的取值范围.
(2)设直线AB的方程为y=kx+m,代入椭圆方程,利用韦达定理,结合k1+k2=4,可得m=k-2,即可证明直线AB过定点,利用△≥0,求出直线AB的斜率k的取值范围.
解答:
(1)解:设|MF1|=m,|MF2|=n,则
∵∠F1MF2=60°,且S△F1MF2=
,
∴16=m2+n2-mn,
mn•
=
,
∴m+n=4
,
∴2a=4
,
∴a=2
,
∵c=2,
∴b=
=4,
∴椭圆C的方程为
+
=1;
(2)证明:设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),则
y=kx+m代入椭圆方程,可得(2k2+1)x2+4kmx+2m2-8=0,
∴x1+x2=-
,x1x2=
,
∵k1+k2=4,
∴
+
=4,
∴m=k-2,
∴直线AB的方程为y=kx+k-2,即y=k(x+1)-2,
∴直线AB过定点(-1,-2).
∵△=(4km)2-4(2k2+1)(2m2-8)≥0,m=k-2,
∴k(7k+4)≥0,
∴k≥0或k≤-
.
∵∠F1MF2=60°,且S△F1MF2=
4
| ||
| 3 |
∴16=m2+n2-mn,
| 1 |
| 2 |
| ||
| 2 |
4
| ||
| 3 |
∴m+n=4
| 2 |
∴2a=4
| 2 |
∴a=2
| 2 |
∵c=2,
∴b=
| a2-c2 |
∴椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)证明:设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),则
y=kx+m代入椭圆方程,可得(2k2+1)x2+4kmx+2m2-8=0,
∴x1+x2=-
| 4km |
| 2k2+1 |
| 2m2-8 |
| 2k2+1 |
∵k1+k2=4,
∴
| kx1+m-2 |
| x1 |
| kx2+m-2 |
| x2 |
∴m=k-2,
∴直线AB的方程为y=kx+k-2,即y=k(x+1)-2,
∴直线AB过定点(-1,-2).
∵△=(4km)2-4(2k2+1)(2m2-8)≥0,m=k-2,
∴k(7k+4)≥0,
∴k≥0或k≤-
| 4 |
| 7 |
点评:本题考查椭圆的方程,考查余弦定理,考查三角形面积的计算,考查韦达定理的运用,考查学生的计算能力,属于难题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
要得到函数y=cos(2x+
)的图象,只需将y=cos2x的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
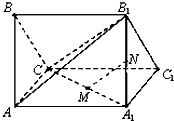 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点. 如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2
如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2 如图,设椭圆
如图,设椭圆