题目内容
6.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=19(a>0,b>0)的离心率为$\frac{\sqrt{5}}{2}$,则C的渐近线方程为( )| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{3}$x | C. | y=±x | D. | y=±$\frac{1}{2}$x |
分析 先根据双曲线的标准方程求得渐近线方程,通过离心率a和c的关系,求得a和b的关系,进而求得渐近线方程.
解答 解:∵双曲线的渐近线方程为y=±$\frac{b}{a}$,离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,可得:$\frac{{a}^{2}+{b}^{2}}{{a}^{2}}=\frac{5}{4}$,解得$\frac{b}{a}=\frac{1}{2}$,
则C的渐近线方程为:y=±$\frac{1}{2}$x.
故选:D.
点评 本题主要考查了双曲线的简单性质.解题的关键是熟练掌握双曲线方程中的a,b和c基本关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知f(x)=x3-ax在(-∞,-1]上是单调函数,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
14.不等式2x2-x-1>0的解集是( )
| A. | $\{x|-\frac{1}{2}<x<1\}$ | B. | {x|x>1} | C. | {x|x<1或x>2} | D. | $\{x|x<-\frac{1}{2}或x>1\}$ |
15.某广告的广告费用x与销售额y的统计数据如表
根据上表可得回归方程中的$\stackrel{∧}{b}$为9.4,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | 39 | 49 | 54 |
| A. | 63.6万元 | B. | 65.5万元 | C. | 67.7万元 | D. | 72.0万元 |
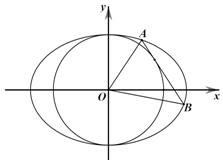 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2