题目内容
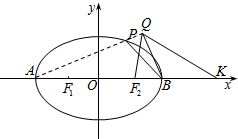
如图,已知椭圆C:
+y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N,
(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;
(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.
| x2 |
| 4 |
(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;
(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.
考点:椭圆的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(ⅰ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论;
(ⅱ)设出以MN为直径的圆上的动点Q的坐标,由
•
=0列式得到圆的方程,化为圆系方程后联立方程组可求解圆所过定点的坐标.
(ⅱ)设出以MN为直径的圆上的动点Q的坐标,由
| QM |
| QN |
解答:
(ⅰ)证明:由题设椭圆C::
+y2=1可知,点A(0,1),B(0,-1).
令P(x0,y0),则由题设可知x0≠0.
∴直线AP的斜率k1=
,PB的斜率为k2=
.
又点P在椭圆上,∴
+y02=1(x0≠1)
从而有k1•k2=
•
=-
;
(ⅱ)解:以MN为直径的圆恒过定点(0,-2+2
)或(0,-2-2
).
事实上,设点Q(x,y)是以MN为直径圆上的任意一点,则
•
=0,
故有(x+
)(x+
)+(y+2)(y+2)=0.
又k1•k2=-
∴以MN为直径圆的方程为x2+(y+2)2-12+(
-4k1)x=0.
令x=0,则(y+2)2=12,解得y=-2±2
.
∴以MN为直径的圆恒过定点(0,-2+2
)或(0,-2-2
).
| x2 |
| 4 |
令P(x0,y0),则由题设可知x0≠0.
∴直线AP的斜率k1=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
又点P在椭圆上,∴
| x02 |
| 4 |
从而有k1•k2=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| 1 |
| 4 |
(ⅱ)解:以MN为直径的圆恒过定点(0,-2+2
| 3 |
| 3 |
事实上,设点Q(x,y)是以MN为直径圆上的任意一点,则
| QM |
| QN |
故有(x+
| 3 |
| k1 |
| 1 |
| k2 |
又k1•k2=-
| 1 |
| 4 |
∴以MN为直径圆的方程为x2+(y+2)2-12+(
| 3 |
| k1 |
令x=0,则(y+2)2=12,解得y=-2±2
| 3 |
∴以MN为直径的圆恒过定点(0,-2+2
| 3 |
| 3 |
点评:本题考查了直线的斜率,考查了直线与圆锥曲线的关系,考查了圆系方程,考查了学生的计算能力,是有一定难度题目.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为4π,为了得到函数g(x)=cosωx的图象,应将f(x)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 椭圆C:
椭圆C: