题目内容
某次数学考试中有三道选做题,分别为选做题1、2、3.规定每位考生必须且只须在其中选做一题.甲、乙、丙三名考生选做这一题中任意一题的可能性均为
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求这三个人选做的是同一道题的概率:
(2)设ξ为三个人中做选做题l的人数,求ξ的分布列与均值.
| 1 |
| 3 |
(1)求这三个人选做的是同一道题的概率:
(2)设ξ为三个人中做选做题l的人数,求ξ的分布列与均值.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:应用题,概率与统计
分析:(1)设事件A1表示三个人选做题1,A2表示三个人选做题2,A3表示三个人选做题3,则这三个人选做的是同一道题事件为A1+A2+A3,根据互斥事件概率乘法公式,可得答案.
(2)ξ可能取值为0,1,2,3.结合甲、乙、丙三名考生选做这一题中任意一题的可能性均为
,可计算出ξ的分布列及数学期望.
(2)ξ可能取值为0,1,2,3.结合甲、乙、丙三名考生选做这一题中任意一题的可能性均为
| 1 |
| 3 |
解答:
解:(1)设事件A1表示三个人选做题1,A2表示三个人选做题2,A3表示三个人选做题3,
则这三个人选做的是同一道题的概率为P(A1+A2+A3)=3×
×
×
=
;
(2)ξ可能取值为0,1,2,3,且5名考生选做这三题的任意一题的可能性均为
,
∴P(ξ=k)=
•(
)k•(
)3-k,k=0,1,2,3,
∴分布列为
∴Eξ=0×
+1×
+2×
+3×
=1.
则这三个人选做的是同一道题的概率为P(A1+A2+A3)=3×
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
(2)ξ可能取值为0,1,2,3,且5名考生选做这三题的任意一题的可能性均为
| 1 |
| 3 |
∴P(ξ=k)=
| C | k 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 8 |
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 1 |
| 27 |
点评:此题考查了离散型随机变量的定义及其分布列,并且利用分布列求出期望,还考查了考虑问题时的严谨的逻辑思维及计算能力.

练习册系列答案
相关题目
设
=(cosx-sinx,2sinx),
=(cosx+sinx,cosx),f(x)=
•
,将函数f(x)的图象平移而得到函数g(x)=
cos2x-1,则平移方法可以是( )
| a |
| b |
| a |
| b |
| 2 |
A、左移
| ||
B、左移
| ||
C、右移
| ||
D、左移
|
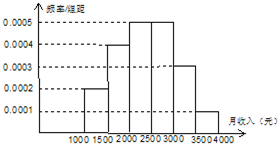 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出