题目内容
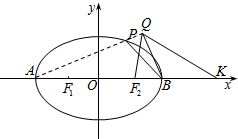 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)若动点Q(x,y)到点F2与到K(8,0)距离之比为
| 1 |
| 2 |
(3)设直线PB,QB的斜率分别为k1,k2,且4k1=3k2,证明:A,P,Q三点共线.
考点:轨迹方程,三点共线,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意结合椭圆定义得到2a+2c=12,从而求出a,再结合c=2求得b,则椭圆方程可求;
(2)直接由动点Q(x,y)到点F2与到K(8,0)距离之比为
列式求点Q的轨迹E的方程;
(3)设P(x0,y0),写出PA和PB的斜率,结合P在椭圆上及4k1=3k2得到kPA•k2=-1,由(2)知点Q在圆x2+y2=16上,由此可得kQA•k2=-1,从而得到PA和QA所在直线的斜率相等,再由两直线有公共点A,可得A,P,Q三点共线.
(2)直接由动点Q(x,y)到点F2与到K(8,0)距离之比为
| 1 |
| 2 |
(3)设P(x0,y0),写出PA和PB的斜率,结合P在椭圆上及4k1=3k2得到kPA•k2=-1,由(2)知点Q在圆x2+y2=16上,由此可得kQA•k2=-1,从而得到PA和QA所在直线的斜率相等,再由两直线有公共点A,可得A,P,Q三点共线.
解答:
(1)解:由椭圆C的焦点为F1(-2,0)得c=2,
又由椭圆的定义得△PF1F2的周长为2a+2c=12,
解得a=4,c=2,
∴b2=a2-c2=12,
即所求椭圆的方程为
+
=1;
(2)解:由题意得
=
,
∵|QF2|=
,|QK|=
,
∴
=
,化简得:x2+y2=16,
经检验得轨迹E的方程为x2+y2=16;
(3)证明:由(1)知A(-4,0),B(4,0),
设P(x0,y0),
则kPA•k1=
•
=
,
∵点P(x0,y0)在椭圆C上,
∴
+
=1,即y02=12-
x02,
∴kPA•k1=
=-
,
∴kPA=-
,
又∵4k1=3k2,
∴kPA•k2=-1,
由(2)知点Q在圆x2+y2=16上,
∴kQA•k2=-1,
∴kPA=kQA,
又直线PA,QA有共同点A,
∴A,P,Q三点共线.
又由椭圆的定义得△PF1F2的周长为2a+2c=12,
解得a=4,c=2,
∴b2=a2-c2=12,
即所求椭圆的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)解:由题意得
| |QF2| |
| |QK| |
| 1 |
| 2 |
∵|QF2|=
| (x-2)2+y2 |
| (x-8)2+y2 |
∴
| ||
|
| 1 |
| 2 |
经检验得轨迹E的方程为x2+y2=16;
(3)证明:由(1)知A(-4,0),B(4,0),
设P(x0,y0),
则kPA•k1=
| y0 |
| x0+4 |
| y0 |
| x0-4 |
| y02 |
| x02-16 |
∵点P(x0,y0)在椭圆C上,
∴
| x02 |
| 16 |
| y02 |
| 12 |
| 3 |
| 4 |
∴kPA•k1=
12-
| ||
| x02-16 |
| 3 |
| 4 |
∴kPA=-
| 3 |
| 4k1 |
又∵4k1=3k2,
∴kPA•k2=-1,
由(2)知点Q在圆x2+y2=16上,
∴kQA•k2=-1,
∴kPA=kQA,
又直线PA,QA有共同点A,
∴A,P,Q三点共线.
点评:本题考查椭圆方程的求法,考查了曲线轨迹方程的求法,训练了平面内三点共线的证明方法,体现了整体运算思想方法,是压轴题.

练习册系列答案
相关题目
 已知F1,F2是椭圆
已知F1,F2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| BF1 |
| 16 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设
=(cosx-sinx,2sinx),
=(cosx+sinx,cosx),f(x)=
•
,将函数f(x)的图象平移而得到函数g(x)=
cos2x-1,则平移方法可以是( )
| a |
| b |
| a |
| b |
| 2 |
A、左移
| ||
B、左移
| ||
C、右移
| ||
D、左移
|