题目内容
曲线C极坐标方程为ρ2-4ρcosθ-4ρsinθ+6=0,以极点为原点,极轴为x轴正半轴建立直角坐标系,直线l的参数方程为
(t为参数),则曲线C上的点到直线l的距离的最小值为 .
|
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程、参数方程化为直角坐标方程,求出圆心到直线的距离,再将此距离减去半径,即得所求.
解答:
解:曲线C极坐标方程为ρ2-4ρcosθ-4ρsinθ+6=0,化为直角坐标方程可得(x-2)2+(y-2)2=2,
表示以(2,2)为圆心、半径r=
的圆.
把直线l的参数方程为
(t为参数)化为直角坐标方程为x+y-1=0,
由于圆心(2,2)到直线的距离d=
=
,
则曲线C上的点到直线l的距离的最小值为d-r=
,
故答案为:
.
表示以(2,2)为圆心、半径r=
| 2 |
把直线l的参数方程为
|
由于圆心(2,2)到直线的距离d=
| |2+2-1| | ||
|
3
| ||
| 2 |
则曲线C上的点到直线l的距离的最小值为d-r=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
相关题目
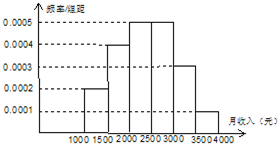 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出