题目内容
在△ABC中,a,b,c分别为内角A,B,C的对边,2asinA=(2b+c)sinB+(2c+b)sinC.
(Ⅰ)求角A的大小
(Ⅱ)求函数f(x)=cos2x-4cosAsinx(x∈R)的值域.
(Ⅰ)求角A的大小
(Ⅱ)求函数f(x)=cos2x-4cosAsinx(x∈R)的值域.
考点:正弦定理,两角和与差的正弦函数,余弦定理
专题:解三角形
分析:(Ⅰ)△ABC中,由条件利用正弦定理求得 b2+c2-a2=-bc.再由余弦定理求得cosA=
的值,可得A的值.
(Ⅱ)利用二倍角的余弦公式化简函数的解析式为f(x)=-2(sinx-
)2+
,再利用二次函数的性质求得函数f(x)的值域.
| b2+c2-a2 |
| 2bc |
(Ⅱ)利用二倍角的余弦公式化简函数的解析式为f(x)=-2(sinx-
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(Ⅰ)△ABC中,∵2asinA=(2b+c)sinB+(2c+b)sinC,
利用正弦定理可得 2a2=2b2+bc+2c2+bc,即 b2+c2-a2=-bc.
再由余弦定理可得 cosA=
=-
,∴A=
.
(Ⅱ)函数f(x)=cos2x-4cosAsinx=cos2x+2sinx=1-2sin2x+2sinx=-2(sinx-
)2+
,
故当sinx=
时,函数f(x)取得最大值为
,当sinx=
=-1时,函数f(x)取得最小值为-3,
故函数f(x)的值域为[-3,
].
利用正弦定理可得 2a2=2b2+bc+2c2+bc,即 b2+c2-a2=-bc.
再由余弦定理可得 cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| 2π |
| 3 |
(Ⅱ)函数f(x)=cos2x-4cosAsinx=cos2x+2sinx=1-2sin2x+2sinx=-2(sinx-
| 1 |
| 2 |
| 3 |
| 2 |
故当sinx=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故函数f(x)的值域为[-3,
| 3 |
| 2 |
点评:本题主要考查正弦定理、余弦定理、正弦函数的值域、二倍角公式、二次函数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

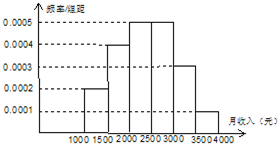 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出