题目内容
设函数y=f(x+1)是偶函数,当x≥1时,f(x)=2x-4,则f(
),f(
),f(
)的大小为 (按由小到大的顺序)
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用函数y=f(x+1)是偶函数,得到函数的对称性,然后利用函数的对称性和函数的单调性进行判断大小.
解答:
解:∵函数y=f(x+1)是偶函数,
∴y=f(-x+1)=f(x+1),即函数f(x)关于x=1对称,
∴f(
)=f(1-
)=f(
+1)=f(
),
f(
)=f(1-
)=f(1+
)=f(
),
∵当x≥1时,f(x)=2x-4,
∴此时函数f(x)单调递增,
∴f(
)<f(
)<f(
),即f(
)<f(
)<f(
),
故答案为:f(
)<f(
)<f(
).
∴y=f(-x+1)=f(x+1),即函数f(x)关于x=1对称,
∴f(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
f(
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∵当x≥1时,f(x)=2x-4,
∴此时函数f(x)单调递增,
∴f(
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
故答案为:f(
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查函数值的大小比较,利用条件确定函数的对称性是解决本题的关键,利用函数的单调性是解决本题的突破点.

练习册系列答案
相关题目
设f:x→log2x是集合A到对应的集合B的映射,若A={1,2,4},则A∩B等于( )
| A、{1} | B、{2} |
| C、{1,2} | D、{1,4} |
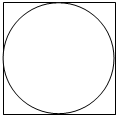 如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )
如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|
已知锐角△ABC的面积为3,BC=4,CA=3,则角C的大小为( )
| A、75° | B、60° |
| C、45° | D、30° |