题目内容
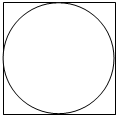如图是一个边长为4的正方形及其内切圆，若随机向正方形内丢一粒豆子，假设豆子不落在线上，则豆子不落入圆内的概率是（ ）A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|
考点：几何概型
专题：概率与统计
分析：根据题意算出正方形的面积和内切圆面积，再利用几何概率公式加以计算，即可得到所求概率．
解答：
解：∵正方形的边长为4，
∴正方形的面积S正方形=16，内切圆的半径r=2，
因此，内切圆的面积为S内切圆=πr2=4π，
可得豆子落入圆内的概率为：P=1-
=1-
．
故选：D．
∴正方形的面积S正方形=16，内切圆的半径r=2，
因此，内切圆的面积为S内切圆=πr2=4π，
可得豆子落入圆内的概率为：P=1-
| S内切圆 |
| S正方形 |
| 4π |
| 16 |
故选：D．
点评：本题给出丢豆子的事件，求豆子落入指定区域的概率．着重考查了正方形、圆面积公式和几何概型的计算等知识，属于基础题．
练习册系列答案
相关题目
不等式x2-3x+2＞0的解集是（ ）
| A、∅ |
| B、R |
| C、（1，2） |
| D、（-∞，1）∪（2，+∞） |
将一个水平放置的正方形ABCD绕直线AB向上转动45°到ABC1D1，再将所得正方形ABC1D1绕直线BC1向上转动45°到A2BC1D2，则平面A2BC1D2与平面ABCD所成二面角的正弦值等于 ．
若f(x)=1-
，则f（2）等于（ ）
| 1 |
| x2 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
设a=log
3，b=(
)0.2，c=2
，则（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、b＞c＞a |
| D、c＞b＞a |