题目内容
函数f(x)=
sin2x-
cos2x-lgx的零点个数为 .
| ||
| 2 |
| 1 |
| 2 |
考点:三角函数中的恒等变换应用,函数零点的判定定理
专题:函数的性质及应用,三角函数的图像与性质
分析:利用三角函数的辅助角公式将函数进行化简,利用函数和方程之间的关系将函数转化为两个函数的图象的交点问题即可得到结论.
解答:
 解:f(x)=
解:f(x)=
sin2x-
cos2x-lgx=sin(2x-
)-lgx,
由f(x)=0得sin(2x-
)=lgx,
设y=sin(2x-
)和y=lgx,
在坐标系中分别作出函数y=sin(2x-
)和y=lgx的图象如图:
由图象可知两个函数的交点个数为5个,
故函数f(x)的零点个数为5,
故答案为:5
 解:f(x)=
解:f(x)=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由f(x)=0得sin(2x-
| π |
| 6 |
设y=sin(2x-
| π |
| 6 |
在坐标系中分别作出函数y=sin(2x-
| π |
| 6 |
由图象可知两个函数的交点个数为5个,
故函数f(x)的零点个数为5,
故答案为:5
点评:本题主要考查三角函数的图象和性质,以及函数与方程的转化,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设a,b,c∈(0,+∞),则三个数a+
,b+
,c+
的值( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、都大于2 |
| B、都小于2 |
| C、至少有一个不大于2 |
| D、至少有一个不小于2 |
已知三个向量
,
,
两两所夹的角都为120°,且|
|=1,|
|=2,|
|=3,则向量
+
与向量
的夹角θ的值为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、30° | B、60° |
| C、120° | D、150° |
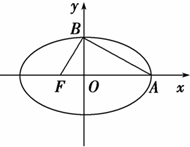 如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )
如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )
用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )