题目内容
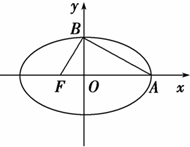 如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )
如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:在三角形AFB中,分别求出AB,FA,FB,再由勾股定理,结合离心率公式以及范围,解方程即可求得双曲线的离心率.
解答:
解:在三角形AFB中,|FB|=
,
|AB|=
=c,|FA|=a+c.
由FB⊥AB,则
(a+c)2=(b2+c2)+c2=3c2-a2,
整理得c2-ac-a2=0,即e2-e-1=0,
解得e=
,
由于双曲线的e>1,
即有e=
.
故选B.
| b2+c2 |
|AB|=
| a2+b2 |
由FB⊥AB,则
(a+c)2=(b2+c2)+c2=3c2-a2,
整理得c2-ac-a2=0,即e2-e-1=0,
解得e=
1±
| ||
| 2 |
由于双曲线的e>1,
即有e=
1+
| ||
| 2 |
故选B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查勾股定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知点P(2,-1)在直线l:ax+y-b=0上的射影是点Q(-2,3),则实数a、b的值依次是( )
| A、-1,5 | B、-1,-5 |
| C、1,5 | D、1,-5 |
已知双曲线的渐近线方程是y=±
x,焦点在x轴上,焦距为20,则它的方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
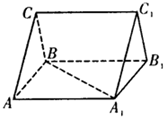
在直三棱柱ABC-A1B1C1中,若
=
,
=
,
=
,则
等于( )
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |

A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|

