题目内容
有下述命题
①若f（a）•f（b）＜0，则函数f（x）在（a，b）内必有零点；
②当a＞1时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax；
③函数y=1（x∈R）是幂函数；
④若A?B，则Card（A）＜Card（B）其中真命题的个数是（ ）
①若f（a）•f（b）＜0，则函数f（x）在（a，b）内必有零点；
②当a＞1时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax；
③函数y=1（x∈R）是幂函数；
④若A?B，则Card（A）＜Card（B）其中真命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：命题的真假判断与应用
专题：函数的性质及应用
分析：①未给出条件：f（x）在区间（a，b）内的连续函数，可知：函数f（x）在（a，b）内不一定有零点；
②当a＞1，n＞0时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax，利用三种函数增长的快慢可知正确；
③函数y=1（x∈R）是常数函数；
④若A?B，则Card（A）与Card（B）大小关系不确定．
②当a＞1，n＞0时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax，利用三种函数增长的快慢可知正确；
③函数y=1（x∈R）是常数函数；
④若A?B，则Card（A）与Card（B）大小关系不确定．
解答：
解：①若f（a）•f（b）＜0，则函数f（x）在（a，b）内不一定有零点，未给出条件：f（x）在区间（a，b）内的连续函数，因此不正确；
②利用结论：当a＞1，n＞0时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax，但是当n≤0时，xn＞logax不成立，因此②不正确；
③函数y=1（x∈R）是常数函数，不是幂函数，因此不正确；
④若A?B，则Card（A）与Card（B）大小关系不确定，因此不正确．
其中真命题的个数是0．
故选：A．
②利用结论：当a＞1，n＞0时，总存在x0∈R，当x＞x0时，总有ax＞xn＞logax，但是当n≤0时，xn＞logax不成立，因此②不正确；
③函数y=1（x∈R）是常数函数，不是幂函数，因此不正确；
④若A?B，则Card（A）与Card（B）大小关系不确定，因此不正确．
其中真命题的个数是0．
故选：A．
点评：本题综合考查了函数零点的判定定理、三种初等函数增长的快慢、幂函数的定义、集合元素的个数等基础知识与基本技能方法，属于基础题．
练习册系列答案
相关题目
从[0，10]中任取一个数x，从[0，6]中任取一个数y，则使|x-5|+|y-3|≤4的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）=（x-1）kcosx（k∈N*），则（ ）
| A、当k=2013时，f（x）在x=1处取得极小值 |
| B、当k=2013时，f（x）在x=1处取得极大值 |
| C、当k=2014时，f（x）在x=1处取得极小值 |
| D、当k=2014时，f（x）在x=1处取得极大值 |
若实数x，y满足
，则实数m=
的取值范围是（ ）
|
| y-1 |
| x+1 |
| A、（-1，1） | ||||
| B、[-1，1） | ||||
C、（-
| ||||
D、[-
|
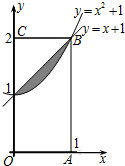如图，在矩形OABC内：记抛物线y=x2+1与直线y=x+1围成的区域为M（图中阴影部分）．随机往矩形OABC内投一点P，则点P落在区域M内的概率是（ ）