题目内容
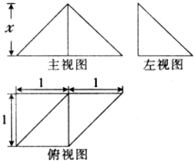
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、6 | ||
B、2
| ||
| C、3 | ||
D、3
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据三视图得出几何体是一个三棱柱，求出它的底面积与高，即得体积．
解答：
解：根据该几何体的三视图知，该几何体是一个平放的三棱柱；
它的底面三角形的面积为S底面=
×2×
=
，
棱柱高为h=3；
∴棱柱的体积为V棱柱=S底面h=
×3=3
；
故选：D．
它的底面三角形的面积为S底面=
| 1 |
| 2 |
| 3 |
| 3 |
棱柱高为h=3；
∴棱柱的体积为V棱柱=S底面h=
| 3 |
| 3 |
故选：D．
点评：本题考查了根据三视图求几何体的体积的问题，解题的关键是由三视图得出几何体是什么几何体，从而作答．
练习册系列答案
阅读快车系列答案
相关题目
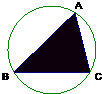如图已知圆的半径为10，其内接三角形ABC的内角A、B分别为60°和45°，现向圆内随机撒一粒豆子，则豆子落在三角形ABC内的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f（x），数列{an}的通项公式是an=f（n），n∈N*，那么“函数y=f（x）在[1，+∞﹚上单调递增”是“数列{an}是递增数列”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f（x）是定义在R上的偶函数，它在[0，+∞）上是减函数．则下列各式一定成立的是（ ）
| A、f（0）＜f（6） |
| B、f（-3）＞f（2） |
| C、f（-1）＞f（3） |
| D、f（-2）＜f（-3） |
已知复数z=
（i为虚数单位），则复数z在复平面内对应的点位于（ ）
| 2i+1 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图所示是一个几何体的三视图，若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|