题目内容
等比数列{an}的首项为a1=2020,公比q=-
.设f(n)表示该数列的前n项的积,则当n= 时,f(n)有最大值.
| 1 |
| 2 |
考点:等比数列的前n项和,等比数列的性质
专题:计算题,等差数列与等比数列
分析:根据等比数列的通项公式,求出f(n),然后即可得到结论.
解答:
解:∵等比数列{an}的首项为a1=2020,公比q=-
.
∴an=a1qn-1=2020(-
)n-1=
•(-1)n-1•212-n.
当n为奇数时an>0,
当n为偶数时,an<0.
=
=an=
•(-1)n-1•212-n.
则|
|=
•212-n,
当n≤11时,|
|>1,此时|f(n)|单调递增,
当n≥12时,|
|<1,此时|f(n)|单调递减,
当n=11时,f(11)<0,
当n=12时,f(12)>0,
∴当n=12时,f(n)有最大值.
故答案为:12.
| 1 |
| 2 |
∴an=a1qn-1=2020(-
| 1 |
| 2 |
| 2020 |
| 2048 |
当n为奇数时an>0,
当n为偶数时,an<0.
| f(n) |
| f(n-1) |
| a1a2???an |
| a1a2???an-1 |
| 2020 |
| 2048 |
则|
| f(n) |
| f(n-1) |
| 2020 |
| 2048 |
当n≤11时,|
| f(n) |
| f(n-1) |
当n≥12时,|
| f(n) |
| f(n-1) |
当n=11时,f(11)<0,
当n=12时,f(12)>0,
∴当n=12时,f(n)有最大值.
故答案为:12.
点评:本题主要考查等比数列通项公式的应用,利用条件判断|
|的单调性是解决本题的关键,综合性较强,难度较大.
| f(n) |
| f(n-1) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知几何体的三视图(如图),若图中圆的半径为1,等腰三角形的腰为3,则该几何体的表面积为
已知几何体的三视图(如图),若图中圆的半径为1,等腰三角形的腰为3,则该几何体的表面积为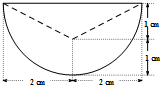 某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是
某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是