题目内容
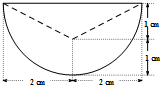 某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是
某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图知几何体为半球挖去一个圆锥,且半球的半径为2,挖去圆锥的高为1,把数据代入体积公式计算.
解答:
解:由三视图知几何体为半球挖去一个圆锥,且半球的半径为2,挖去圆锥的高为1,
∴几何体的体积V=
π×23-
×π×22×1=4π(cm3).
故答案是4π.
∴几何体的体积V=
| 2 |
| 3 |
| 1 |
| 3 |
故答案是4π.
点评:本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及三视图的数据所对应的几何量.

练习册系列答案
相关题目
下列函数中,在区间(0,2)上是增函数的是( )
| A、y=x2-4x+5 | ||
B、y=
| ||
| C、y=2-x | ||
D、y=log
|
已知点(-3,1)和(0,-2)在直线x-y-a=0的一侧,则a的取值范围是( )
| A、(-2,4) |
| B、(-4,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-4)∪(2,+∞) |