题目内容
已知数列{an}是公差为d的等差数列,{bn}是等比数列,函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.
(Ⅰ)求a6的值;
(Ⅱ)若d≠0且f(a2+a8)=f(a3+a11),求数列{bn}的通项公式bn;
(Ⅲ)设Tn=
+
+…+
(n≥6),若Tn的最小值为2,求d的值.
| 7 |
| 2 |
(Ⅰ)求a6的值;
(Ⅱ)若d≠0且f(a2+a8)=f(a3+a11),求数列{bn}的通项公式bn;
(Ⅲ)设Tn=
| 1 |
| a6a7 |
| 1 |
| a7a8 |
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由于函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.可得b3=-4,且当x=-
时,函数f(x)取得最大值
=b3-
b3=a6-
,解得a6.
(Ⅱ)由f(a2+a8)=f(a3+a11),可得
=-
.化为-
=
,即可解得
.
(Ⅲ)Tn=
+
+…+
=
[(
-
)+(
-
)+…+(
-
)]=
(
-
)=
,可知:当n=6时,Tn取得最小值
=2,解得d即可.
| 7 |
| 2 |
| b2 |
| 2b1 |
4b1b3-
| ||
| 4b1 |
| 1 |
| 4 |
| 7 |
| 2 |
(Ⅱ)由f(a2+a8)=f(a3+a11),可得
| a2+a8+a3+a11 |
| 2 |
| b2 |
| 2b1 |
| b2 |
| 2b1 |
| 4a6 |
| 2 |
| b2 |
| b1 |
(Ⅲ)Tn=
| 1 |
| a6a7 |
| 1 |
| a7a8 |
| 1 |
| anan+1 |
| 1 |
| d |
| 1 |
| a6 |
| 1 |
| a7 |
| 1 |
| a7 |
| 1 |
| a8 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| d |
| 1 |
| a6 |
| 1 |
| an+1 |
| 4(n-5) |
| 1+2(n-5)d |
| 4 |
| 1+2d |
解答:
解:(Ⅰ)∵函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,其最大值为a6-
.
∴b3=-4,当x=-
时,函数f(x)取得最大值
=b3-
b3=-4+1=-3=a6-
,
解得a6=
.
(Ⅱ)∵f(a2+a8)=f(a3+a11),
∴
=-
.∴-
=
=2a6=1,
∴公比q=
=-2.
∴数列{bn}的通项公式bn=b3•qn-3=-4×(-2)n-3=-(-2)n-1.
(Ⅲ)Tn=
+
+…+
=
[(
-
)+(
-
)+…+(
-
)]=
(
-
)=
[
-
]=
,
当n=6时,Tn取得最小值
=2,解得d=
.
| 7 |
| 2 |
∴b3=-4,当x=-
| b2 |
| 2b1 |
4b1b3-
| ||
| 4b1 |
| 1 |
| 4 |
| 7 |
| 2 |
解得a6=
| 1 |
| 2 |
(Ⅱ)∵f(a2+a8)=f(a3+a11),
∴
| a2+a8+a3+a11 |
| 2 |
| b2 |
| 2b1 |
| b2 |
| 2b1 |
| 4a6 |
| 2 |
∴公比q=
| b2 |
| b1 |
∴数列{bn}的通项公式bn=b3•qn-3=-4×(-2)n-3=-(-2)n-1.
(Ⅲ)Tn=
| 1 |
| a6a7 |
| 1 |
| a7a8 |
| 1 |
| anan+1 |
| 1 |
| d |
| 1 |
| a6 |
| 1 |
| a7 |
| 1 |
| a7 |
| 1 |
| a8 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| d |
| 1 |
| a6 |
| 1 |
| an+1 |
| 1 |
| d |
| 1 | ||
|
| 1 | ||
|
| 4(n-5) |
| 1+2(n-5)d |
当n=6时,Tn取得最小值
| 4 |
| 1+2d |
| 1 |
| 2 |
点评:本题综合考查了二次函数的性质、等差数列与等比数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知F1、F2椭圆
+
=1左右焦点,P是椭圆是一点,|PF1|=5,则∠F2PF1的大小为( )
| x2 |
| 16 |
| 4y2 |
| 15 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)满足f(x)=f(
),且当x∈[
,1]时,f(x)=lnx,若当x∈[
,e]时,函数g(x)=f(x)-ax与x轴有两个相异交点,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| e |
| 1 |
| e |
| A、[-e,0) | ||
| B、[-e,0] | ||
C、[-
| ||
D、[-e,-
|
若f(x)=x2+2xf′(1),则f′(0)=( )
| A、1 | B、2 | C、-4 | D、6 |
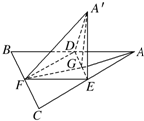 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是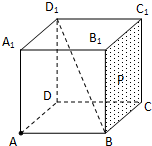 如图,棱长为1的正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持向量
如图,棱长为1的正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持向量