Question

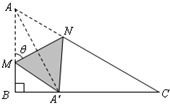如图，直角三角形ABC中，∠B=90°，AB=1，BC=

3

．点M，N分别在边AB和AC上（M点和B点不重合），将△AMN沿MN翻折，△AMN变为△A′MN，使顶点A′落在边BC上（A′点和B点不重合）．设∠AMN=θ．
（Ⅰ）用θ表示线段AM的长度，并写出θ的取值范围；
（Ⅱ）求线段A′N长度的最小值．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：（1）设MA=MA'=x，则MB=1-x，在Rt△MBA'中，利用三角函数可求；
（2）求线段A'N长度的最小值，即求线段AN长度的最小值，再利用三角恒等变换化简，从而求最值．

解答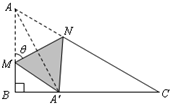： 解：（I）易知△AMN≌△A′MN，∴∠A′MA=2θ，
则∠A′MB=180°-2θ，∠BA′M=90°-（180°-2θ）=2θ-90°，
设MA=MA′=x，则MB=1-x，
在Rt△MBA′中，sin（2θ-90°）=-cos2θ=

1-x

x

，
∴MA=x=

1

1-cos2θ

=

1

2sin2θ

，
∵点M在线段AB上，M点和B点不重合，A′点和B点不重合，
∴45°＜θ＜90°；
（II）在△AMN中，由∠AMN=θ，可得∠ANM=

2π

3

-θ
∴根据正弦定理得：

AN

sinθ

=

MA

sin( 2π 3 -θ)

，
∴AN=

1

2sinθsin( 2π 3 -θ)

令t=2sinθsin（120°-θ）=2sinθ（

1

2

sinθ+

3

2

cosθ）
=sin²θ+

3

sinθcosθ=

1

2

+

3

2

sin2θ-

1

2

cos2θ=

1

2

+sin（2θ-30°），
∵45°＜θ＜90°，∴60°＜2θ-30°＜150°，
当且仅当2θ-30°=90°，θ=60°时，t有最大值

3

2

，
则θ=60°时，AN有最小值为

2

3

，即线段A′N长度的最小值为

2

3

．

点评：本题主要考查在实际问题中建立三角函数模型，从而利用三角函数中研究最值的方法解决最值问题，应注意角的范围的确定是关键．