题目内容
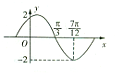已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤| π |
| 2 |
| π |
| 6 |
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由图象顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，从而得到函数的解析式，从而求得f（
）的值．
| π |
| 6 |
解答：
解：由图象顶点的坐标可得A=2，
•T=
•
=
-
，∴ω=2．
再由五点法作图可得2×
+φ=π，∴φ=
，∴f（x）=2sin（2x+
），
∴f（
）=2sin（2×
+
）=2×
=
，
故选：B．
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再由五点法作图可得2×
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f（
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| ||
| 2 |
| 3 |
故选：B．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
将某组样本数据按[7.5，8.5），[8.5，9.5），[9.5，10.5]分成3组，其频率分布直方图如图所示，由此估计这组样本数据的中位数是
已知集合 A={x|x2+x-2≤0}，B={x|-2≤x≤a}，若A∩B≠∅，则（ ）
| A、a＞-2 | B、a≥-2 |
| C、a＞1 | D、a≥1 |
已知集合M={y|y=（
）x，x∈R}，N={1，0，-1}，则M∩N=（ ）
| 1 |
| 3 |
| A、{1，0，-1} |
| B、{1，-1} |
| C、{1，0} |
| D、{1} |
已知等比数列{an}的各项都为正数，且以a1+a2＞2a3，则公比q的取值范围是（ ）
A、（0，
| ||
B、（
| ||
| C、（0，1） | ||
| D、（1，+∞） |
若某物体的三视图如图所示，则该物体的体积是（ ）
| A、10+6π |
| B、10+20π |
| C、14+5π |
| D、14+20π |
已知集合A={x|x2-3x＜0}，B={x|log3（x-1）＜1}，则下列结论中正确的是（ ）
| A、2∈A∩B且1∈A∪B |
| B、2∈A∩B且1∉A∪B |
| C、2∉A∩B且1∈A∪B |
| D、2∉A∩B且1∉A∪B |
如图，△ABC内接于圆O，∠A的平分线交BC于点D，交外接圆于点E，求证：AD2=AB•AC-BD•DC．