题目内容
19.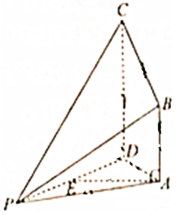 如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.
如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.(Ⅰ)求证:AE∥平面PBC;
(Ⅱ)求证:平面PBC⊥平面PCD.
分析 (Ⅰ)取PC的中点F,连接EF,BF,证明EF∥CD,EF∥AB,推出AE∥BF.然后证明AE∥平面PBC.
(Ⅱ)证明CD⊥AE,AE⊥PD.推出AE⊥平面PCD,顶点BF⊥平面PCD,然后证明平面PBC⊥平面PCD.
解答 证明:(Ⅰ)取PC的中点F,连接EF,BF,…(1分)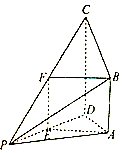
因为E,F分别是PD,PC的中点,所以EF∥CD,且$EF=\frac{1}{2}CD$. …(2分)
又AB∥CD,$AB=\frac{1}{2}CD$,
所以EF∥AB,且EF=AB,…(3分)
即四边形ABFE为平行四边形,…(4分)
所以AE∥BF. …(5分)
因为BF?平面PBC,且AE?平面PBC,…(6分)
所以AE∥平面PBC. …(7分)
(Ⅱ)因为CD⊥平面APD,AE?平面APD,所以CD⊥AE,…(8分)
因为AD=AP,E为PD的中点,
所以AE⊥PD. …(9分)
又PD∩CD=D,
所以AE⊥平面PCD,…(10分)
由(Ⅰ)知,BF∥AE,
所以BF⊥平面PCD,…(11分)
又BF?平面PBC,
所以平面PBC⊥平面PCD. …(12分)
点评 本题考查直线与平面垂直与平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
9.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
10.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )


| A. | 36π | B. | 24π | C. | 12π | D. | 6π |
7.已知命题p:若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$;命题q:若m>1,则函数 y=x2+mx+1有两个零点.在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,为真命题的是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
11.阅读如图程序框图,如果输出k=5,那么空白的判断框中应填入的条件是( )


| A. | S>-25 | B. | S<-26 | C. | S<-25 | D. | S<-24 |
9.i为虚数单位,若复数z=(1-ai)(1+i)(a∈R)的虚部为-3,则|z|=( )
| A. | $3\sqrt{2}$ | B. | 4 | C. | $\sqrt{34}$ | D. | 5 |