题目内容
7.已知命题p:若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$;命题q:若m>1,则函数 y=x2+mx+1有两个零点.在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,为真命题的是( )| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
分析 先判断命题p,q的真假,再由复合命题真假判断的真值表,可得答案.
解答 解:函数f(x)=${(\frac{1}{2})}^{x}$为减函数,
若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$,
故命题p:为真命题;
m>1时,x2+mx+1=0不一定有两个根,
则命题q:函数 y=x2+mx+1有两个零点为假命题.
则:(1)p∧q为假命题;
(2)p∨q为真命题;
(3)p∧(¬q)为真命题;
(4)(¬p)∨q为假命题,
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数的图象和性质,方程根的存在性与个数判断等知识点,难度中档.

练习册系列答案
相关题目
18.已知△ABC中,$AC=2,AB=2\sqrt{7},cos∠BAC=\frac{{2\sqrt{7}}}{7}$且D是BC的中点,则中线AD的长为( )
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
2.对于实数m>-3,若函数$y={(\frac{1}{2})^x}$图象上存在点(x,y)满足约束条件$\left\{\begin{array}{l}x-y+3≥0\\ x+2y+3≥0\\ x≤m\end{array}\right.$,则实数m 的最小值为( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
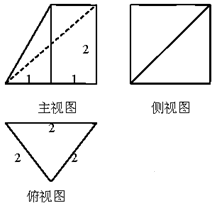

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
17.已知向量$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(1,m-$\frac{3}{2}$),$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | 3 | B. | 0 | C. | $\frac{13}{6}$ | D. | $\frac{3}{2}$ |
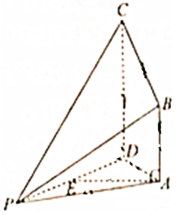 如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.
如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.