题目内容
14.设向量$\overrightarrow a$=(x,2),$\overrightarrow b$=(1,-1),且$(\overrightarrow a-\overrightarrow b)⊥\overrightarrow b$,则x 的值是4.分析 $(\overrightarrow a-\overrightarrow b)⊥\overrightarrow b$,可得($\overrightarrow{a}-\overrightarrow{b}$)$•\overrightarrow{b}$=0,解出即可得出.
解答 解:$\overrightarrow{a}-\overrightarrow{b}$=(x-1,3),
∵$(\overrightarrow a-\overrightarrow b)⊥\overrightarrow b$,
∴($\overrightarrow{a}-\overrightarrow{b}$)$•\overrightarrow{b}$=x-1-3=0,解得x=4.
故答案为:4.
点评 本题考查了向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.i为虚数单位,复数$\frac{3+i}{1-i}$的虚部是( )
| A. | 2i | B. | 2 | C. | -2i | D. | -1 |
2.对于实数m>-3,若函数$y={(\frac{1}{2})^x}$图象上存在点(x,y)满足约束条件$\left\{\begin{array}{l}x-y+3≥0\\ x+2y+3≥0\\ x≤m\end{array}\right.$,则实数m 的最小值为( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |
9.从六个数1,3,4,6,7,9中任取2个数,则这两个数的平均数恰好是5的概率为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
6.某人打算制定一个长期储蓄计划,每年年初存款2万元,连续储蓄12年.由于资金原因,从第7年年初开始,变更为每年年初存款1万元.若存款利率为每年2%,且上一年年末的本息和共同作为下一年年初的本金,则第13年年初时的本息和约为( )万元(结果精确到0.1).(参考数据:1.026≈1.13,1.0212≈1.27)
| A. | 20.09万元 | B. | 20.50万元 | C. | 20.91万元 | D. | 21.33万元 |
3.设x,y满足约束条件$\left\{\begin{array}{l}{x≥y}\\{y≥4x-3}\\{x≥0,y≥0}\end{array}\right.$,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$后的表达式为( )
| A. | y=tan(2x+$\frac{π}{6}$) | B. | y=tan(x-$\frac{π}{6}$) | C. | y=tan(2x-$\frac{π}{6}$) | D. | y=tan2x |
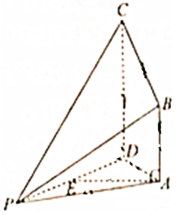 如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.
如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.