题目内容

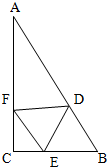某个公园有个池塘，其形状为直角△ABC，∠C=90°，AB=200米，BC=100米．现在准备新建造一个荷塘，分别在AB，BC，CA上取点D，E，F，建造△DEF连廊（不考虑宽度）供游客休憩，且使△DEF为正三角形，设求△DEF边长的最小值．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：设正三角形DEF的边长为a、∠CEF=α且∠EDB=∠1，将CF和AF用a、α表示出，再用α分别分别表示出∠1和∠ADF，然后利用正弦定理表示a并结合辅角公式化简，利用正弦函数的值域即可求得a的最小值．
解答： 解：设正△DEF的边长为a，∠CEF=α
则CF=a•sinα，AF=
3
-a•sinα
设∠EDB=∠1，可得
∠1=180°-∠B-∠DEB=120°-∠DEB，α=180°-60°-∠DEB=120°-∠DEB
∴∠ADF=180°-60°-∠1=120°-α
在△ADF中，
a
sin30°
=
3
-asinα
sin∠ADF
，
化简得a[2sin（120°-α）+sinα]=
3

∴a=
3
2sinα+
3
cosα
=
3
7
sin(α+φ)
≥
21
7
（其中φ是满足tanφ=
3
2
的锐角）
∴△DEF边长最小值为
21
7
．
点评：本题着重考查了解直角三角形、正弦定理和三角恒等变换等知识，考查了在实际问题中建立三角函数模型能力，属于中档题．
练习册系列答案
相关题目
在数列{an}中，a1=14，3an=3an+1+2，则使anan+2＜0成立的n值是（　　）
A、21B、22C、23D、24
已知复数z=
3-bi
1-2i
（i是虚数单位）的实部和虚部相等，则b=
 
．
已知f（x）=x2+bx+c（b，c∈R），g（x）=4-x-m•（2-x）-9（m∈R），A={x|f（x）=x-2}．
（1）若A={1}，解不等式f（x）＞1；
（2）若b∈Z，-3∈A，x1，x2为方程f（x）=0的两个实根，且
4
x1
+
1
x2
=-
1
2
，
①求b，c的值
②若对任意的t1∈[-2，2]，总存在t2∈[-2，2]，使得f（t1）=g（t2）成立，求m的取值范围．
已知两条不同的直线m，n和两个不同的平面α，β，以下四个结论中正确的个数为（　　）
①若m∥α，n∥β，且α∥β，则m∥n；  
②若m∥α，n⊥β，且α⊥β，则m∥n；
③若m⊥α，n∥β，且α∥β，则m⊥n； 
④若m⊥α，n⊥β，且α⊥β，则m⊥n．
A、1个B、2个C、3个D、4个
已知抛物线C1：x2=y，圆C2：x2+（y-4）2=1．
（1）在抛物线C1上取点M，C2的圆周取一点N，求|MN|的最小值；
（2）设P（x0，y0）（2≤x0≤4）为抛物线C1上的动点，过P作圆C2的两条切线，交抛物线C1于A，B两点．求AB的中点D的横坐标的取值范围．
设函数f（x）=cos2x-
3
2
sin2x，若α∈（
π
4
，
π
2
）且满足f（α）=
1
2
-
3
2
，求tan2α的值．
试比较下列各式的大小（不写过程）
（1）1-
2
与
2
-
3

（2）
2
-
3
与
3
-
4

通过上式请你推测出
n-1
-
n
与
n
-
n+1
(n≥2且n∈N）的大小，并用分析法加以证明．
已知正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）的底面边长为a，侧棱长为
2
a
（1）求它的外接球的体积
（2）求他的内切球的表面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网